Title: “Search for an Excess of Electron Neutrino Interactions in MicroBooNE Using Multiple Final State Topologies”
Authors: The MiniBoone Collaboration
Reference: https://arxiv.org/abs/2110.14054
This is the first post in a series on the latest MicroBooNE results, covering the experimental side. Click here to read about the theory side.
The new results from the MicroBoone experiment received a lot of excitement last week, being covered by several major news outlets. But unlike most physics news stories that make the press, it was a null result; they did not see any evidence for new particles or interactions. So why is it so interesting? Particle physics experiments produce null results every week, but what made this one newsworthy is that MicroBoone was trying to check the results from two previous experiments LSND and MiniBoone, that did see something anomalous with very high statistical evidence. If the LSND/MiniBoone result was confirmed, it would have been a huge breakthrough in particle physics, but now that it wasn’t many physicists are scratching their heads trying to make sense of these seemingly conflicting results. However, the MicroBoone experiment is not exactly the same as MiniBoone/LSND, and understanding the differences between the two sets of experiments may play an important role in unraveling this mystery.
Accelerator Neutrino Basics
All of these experiments are ‘accelerator neutrino experiments’, so lets first review what that means. Neutrino’s are ‘ghostly’ particles that are difficult to study (check out this post for more background on neutrinos). Because they only couple through the weak force, neutrinos don’t like to interact with anything very much. So in order to detect them you need both a big detector with a lot of active material and a source with a lot of neutrinos. These experiments are designed to detect neutrinos produced in a human-made beam. To make the beam, a high energy beam of protons is directed at a target. These collisions produce a lot of particles, including unstable bound states of quarks like pions and kaons. These unstable particles have charge, so we can use magnets to focus them into a well-behaved beam. When the pions and kaons decay they usually produce a muon and a muon neutrino. The beam of pions and kaons is pointed at an underground detector located a few hundred meters (or kilometers!) away, and then given time to decay. After they decay there will be a nice beam of muons and muon neutrinos. The muons can be stopped by some kind of shielding (like the earth’s crust), but the neutrinos will sail right through to the detector.

Nearly all of the neutrinos from the beam will still pass right through your detector, but a few of them will interact, allowing you to learn about their properties.
All of these experiments are considered ‘short-baseline’ because the distance between the neutrino source and the detector is only a few hundred meters (unlike the hundreds of kilometers in other such experiments). These experiments were designed to look for oscillation of the beam’s muon neutrinos into electron neutrinos which then interact with their detector (check out this post for some background on neutrino oscillations). Given the types of neutrinos we know about and their properties, this should be too short of a distance for neutrinos to oscillate, so any observed oscillation would be an indication something new (beyond the Standard Model) was going on.
The LSND + MiniBoone Anomaly
So the LSND and MiniBoone ‘anomaly’ was an excess of events above backgrounds that looked like electron neutrinos interacting with their detector. Both detectors were based on similar technology and were a similar distance from their neutrino source. Their detectors were essentially big tanks of mineral oil lined with light-detecting sensors.

At these energies the most common way neutrinos interact is to scatter against a neutron to produce a proton and a charged lepton (called a ‘charged current’ interaction). Electron neutrinos will produce outgoing electrons and muon neutrinos will produce outgoing muons.
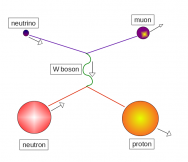
When traveling through the mineral oil these charged leptons will produce a ring of Cherenkov light which is detected by the sensors on the edge of the detector. Muons and electrons can be differentiated based on the characteristics of the Cherenkov light they emit. Electrons will undergo multiple scatterings off of the detector material while muons will not. This makes the Cherenkov rings of electrons ‘fuzzier’ than those of muons. High energy photons can produce electrons positron pairs which look very similar to a regular electron signal and are thus a source of background.

Even with a good beam and a big detector, the feebleness of neutrino interactions means that it takes a while to get a decent number of potential events. The MiniBoone experiment ran for 17 years looking for electron neutrinos scattering in their detector. In MiniBoone’s most recent analysis, they saw around 600 more events than would be expected if there were no anomalous electron neutrinos reaching their detector. The statistical significance of this excess, 4.8-sigma, was very high. Combining with LSND which saw a similar excess, the significance was above 6-sigma. This means its very unlikely this is a statistical fluctuation. So either there is some new physics going on or one of their backgrounds has been seriously under-estimated. This excess of events is what has been dubbed the ‘MiniBoone anomaly’.

The MicroBoone Result
The MicroBoone experiment was commissioned to verify the MiniBoone anomaly as well as test out a new type of neutrino detector technology. The MicroBoone is the first major neutrino experiment to use a ‘Liquid Argon Time Projection Chamber’ detector. This new detector technology allows more detailed reconstruction of what is happening when a neutrino scatters in the detector. The the active volume of the detector is liquid Argon, which allows both light and charge to propagate through it. When a neutrino scatters in the liquid Argon, scintillation light is produced that is collected in sensors. As charged particles created in the collision pass through the liquid Argon they ionize atoms they pass by. An electric field applied to the detector causes this produced charge to drift towards a mesh of wires where it can be collected. By measuring the difference in arrival time between the light and the charge, as well as the amount of charge collected at different positions and times, the precise location and trajectory of the particles produced in the collision can be determined.

This means that unlike the MiniBoone and LSND, MicroBoone can see not just the lepton, but also the hadronic particles (protons, pions, etc) produced when a neutrino scatters in their detector. This means that the same type of neutrino interaction actually looks very different in their detector. So when they went to test the MiniBoone anomaly they adopted multiple different strategies of what exactly to look for. In the first case they looked for the type of interaction that an electron neutrino would have most likely produced: an outgoing electron and proton whose kinematics match those of a charged current interaction. Their second set of analyses, designed to mimic the MiniBoone selection, are slightly more general. They require one electron and any number of protons, but no pions. Their third analysis is the most general and requires an electron along with anything else.
These different analyses have different levels of sensitivity to the MiniBoone anomaly, but all of them are found to be consistent with a background-only hypothesis: there is no sign of any excess events. Three out of four of them even see slightly less events than the expected background.

Overall the MicroBoone data rejects the hypothesis that the MiniBoone anomaly is due to electron neutrino charged current interactions at quite high significance (>3sigma). So if its not electron neutrinos causing the MiniBoone anomaly, what is it?
What’s Going On?
Given that MicroBoone did not see any signal, many would guess that MiniBoone’s claim of an excess must be flawed and they have underestimated one of their backgrounds. Unfortunately it is not very clear what that could be. If you look at the low-energy region where MiniBoone has an excess, there are three major background sources: decays of the Delta baryon that produce a photon (shown in tan), neutral pions decaying to pairs of photons (shown in red), and backgrounds from true electron neutrinos (shown in various shades of green). However all of these sources of background seem quite unlikely to be the source of the MiniBoone anomaly.
Before releasing these results, MicroBoone performed a dedicated search for Delta baryons decaying into photons, and saw a rate in agreement with the theoretical prediction MiniBoone used, and well below the amount needed to explain the MiniBoone excess.
Backgrounds from true electron neutrinos produced in the beam, as well as from the decays of muons, should not concentrate only at low energies like the excess does, and their rate has also been measured within MiniBoone data by looking at other signatures.
The decay of a neutral pions can produce two photons, and if one of them escapes detection, a single photon will mimic their signal. However one would expect that it would be more likely that photons would escape the detector near its edges, but the excess events are distributed uniformly in the detector volume.
So now the mystery of what could be causing this excess is even greater. If it is a background, it seems most likely it is from an unknown source not previously considered. As will be discussed in our part 2 post, its possible that MiniBoone anomaly was caused by a more exotic form of new physics; possibly the excess events in MiniBoone were not really coming from the scattering of electron neutrinos but something else that produced a similar signature in their detector. Some of these explanations included particles that decayed into pairs of electrons or photons. These sorts of explanations should be testable with MicroBoone data but will require dedicated analyses for their different signatures.
So on the experimental side, we now we are left to scratch our heads and wait for new results from MicroBoone that may help get to the bottom of this.
Click here for part 2 of our MicroBoone coverage that goes over the theory side of the story!
Read More
“Is the Great Neutrino Puzzle Pointing to Multiple Missing Particles?” – Quanta Magazine article on the new MicroBoone result
“Can MiniBoone be Right?” – Resonaances blog post summarizing the MiniBoone anomaly prior to the the MicroBoone results
A review of different types of neutrino detectors – from the T2K experiment














