Neutrinos: What Do They Know? Do They Know Things?

Title: “Upper Bound of Neutrino Masses from Combined Cosmological Observations and Particle Physics Experiments”

Author: Loureiro et al. 

Reference: https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.123.081301

Neutrinos are almost a lot of things. They are almost massless, a property that goes against the predictions of the Standard Model. Possessing this non-zero mass, they should travel at almost the speed of light, but not quite, in order to be consistent with the principles of special relativity. Yet each measurement of neutrino propagation speed returns a value that is, within experimental error, exactly the speed of light. Only coupled to the weak force, they are almost non-interacting, with 65 billion of them streaming from the sun through each square centimeter of Earth each second, almost undetected. 

How do all of these pieces fit together? The story of the neutrino begins in 1930, when Wolfgang Pauli propositioned an as-yet detected particle emitted during beta decay in order to explain an observed lack of energy and momentum conservation. In 1956, an antineutrino-positron annihilation producing two gamma rays was detected, confirming the existence of neutrinos. Yet with this confirmation came an assortment of growing mysteries. In the decades that followed, a series of experiments found that there are three distinct flavors of neutrino, one corresponding to each type of lepton: electron, muon, and tau particles. Subsequent measurements of propagating neutrinos then revealed a curious fact: these three flavors are anything but distinct. When the flavor of a neutrino is initially measured to be, say, an electron neutrino, a second measurement of flavor after it has traveled some distance could return the answer of muon neutrino. Measure yet again, and you could find yourself a tau neutrino. This process, in which the probability of measuring a neutrino in one of the three flavor states varies as it propagates, is known as neutrino oscillation. 

Neutrino oscillation threw a wrench into the Standard Model in terms of mass; neutrino oscillation implies that the masses of the three neutrino flavors cannot be equal to each other, and hence cannot all be zero. Specifically, only one of them would be allowed to be zero, with the remaining two non-zero and non-equal. While at first glance an oddity, oscillation arises naturally from underlying mathematics, and we can arrive at this conclusion via a simple analysis. To think about a neutrino, we consider two eigenstates (the state a particle is in when it is measured to have a certain observable quantity), one corresponding to flavor and one corresponding to mass. Because neutrinos are created in weak interactions which conserve flavor, they are initially in a flavor eigenstate. Flavor and mass eigenstates cannot be simultaneously determined, and so each flavor eigenstate is a linear combination of mass eigenstates, and vice versa. Now, consider the case of three flavors of neutrino. If all three flavors consisted of the same linear combination of mass eigenstates, there would be no varying superposition between them, since the different masses would travel at different speeds in accordance with special relativity. Since we experimentally observe an oscillation between neutrino flavors, we can conclude that their masses cannot all be the same.

Although this result was unexpected and provides the first known departure from the Standard Model, it is worth noting that it also neatly resolves a few outstanding experimental mysteries, such as the solar neutrino problem. Neutrinos in the sun are produced as electron neutrinos and are likely to interact with unbound electrons as they travel outward, transitioning them into a second mass state which can interact as any of the three flavors. By observing a solar neutrino flux roughly a third of its predicted value, physicists not only provided a potential answer to a previously unexplained phenomenon but also deduced that this second mass state must be larger than the state initially produced. Related flux measurements of neutrinos produced during charged particle interactions in the Earth’s upper atmosphere, which are primarily muon neutrinos, reveal that the third mass state is quite different from the first two mass states. This gives rise to two potential mass hierarchies: the normal () and inverted () ordering.

However, this oscillation also means that it is difficult to discuss neutrino masses individually, as measuring the sum of neutrino masses is currently easier from a technical standpoint. With current precision in cosmology, we cannot distinguish the three neutrinos at the epoch in which they become free-traveling, although this could change with increased precision. Future experiments in beta decay could also lead to progress in pinpointing individual masses, although current oscillation experiments are only sensitive to mass-squared differences . Hence, we frame our models in terms of these mass splittings and the mass sum, which also makes it easier to incorporate cosmological data. Current models of neutrinos are phenomenological ― not directly derived from theory but consistent with both theoretical principles and experimental data. The mixing between states is mathematically described by the PMNS (Pontecorvo-Maki-Nakagawa-Sakata) matrix, which is parametrized by three mixing angles and a phase related to CP violation. These parameters, as in most phenomenological models, have to be inserted into the theory. There is usually a wide space of parameters in such models and constraining this space requires input from a variety of sources. In the case of neutrinos, both particle physics experiments and cosmological data provide key avenues for exploration into these parameters. In a recent paper, Loureiro et al. used such a strategy, incorporating data from the large scale structure of galaxies and the cosmic microwave background to provide new upper bounds on the sum of neutrino masses.

The group investigated two main classes of neutrino mass models: exact models and cosmological approximations. The former concerns models that integrate results from neutrino oscillation experiments and are parametrized by the smallest neutrino mass, while the latter class uses a model scheme in which the neutrino mass sum is related to an effective number of neutrino species times an effective mass which is equal for each flavor. In exact models, Gaussian priors (an initial best-guess) were used with data sampling from a number of experimental results and error bars, depending on the specifics of the model in question. This includes possibilities such as fixing the mass splittings to their central values or assuming either a normal or inverted mass hierarchy. In cosmological approximations, was fixed to a specific value depending on the particular cosmological model being studied, with the total mass sum sampled from data.

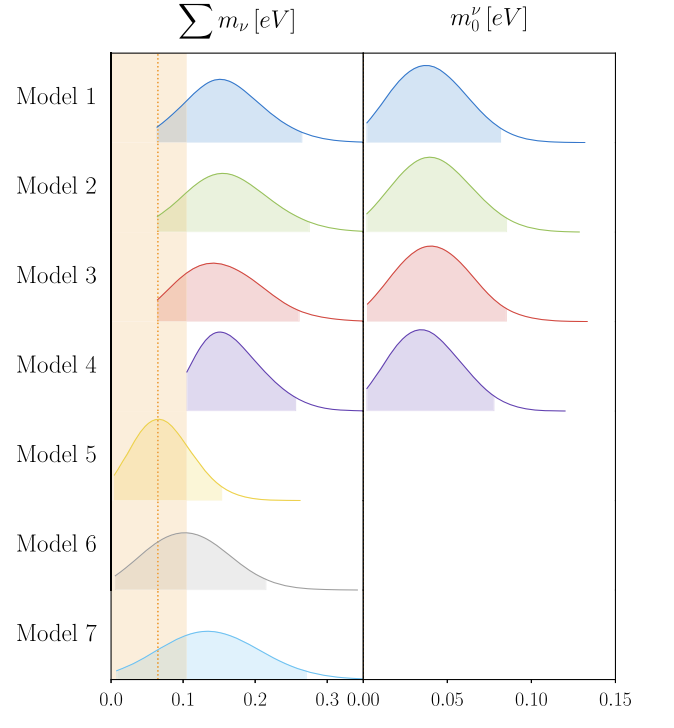
The group ultimately demonstrated that cosmologically-based models result in upper bounds for the mass sum that are much lower than those generated from physically-motivated exact models, as we can see in the figure above. One of the models studied resulted in an upper bound that is not only different from those determined from neutrino oscillation experiments, but is inconsistent with known lower bounds. This puts us into the exciting territory that neutrinos have pushed us to again and again: a potential finding that goes against what we presently know. The calculated upper bound is also significantly different if the assumption is made that one of the neutrino masses is zero, with the mass sum contained in the remaining two neutrinos, setting the stage for future differentiation between neutrino masses. Although the group did not find any statistically preferable model, they provide a framework for studying neutrinos with a considerable amount of cosmological data, using results of the Planck, BOSS, and SDSS collaborations, among many others. Ultimately, the only way to arrive at a robust answer to the question of neutrino mass is to consider all of these possible sources of information for verification. 

With increased sensitivity in upcoming telescopes and a plethora of intriguing beta decay experiments on the horizon, we should be moving away from studies that update bounds and toward ones which make direct estimations. In these future experiments, previous analysis will prove vital in working toward an understanding of the underlying mass models and put us one step closer to unraveling the enigma of the neutrino. While there are still many open questions concerning their properties ― Why are their masses so small? Is the neutrino its own antiparticle? What governs the mass mechanism? ― studies like these help to grow intuition and prepare for the next phases of discovery. I’m excited to see what unexpected results come next for this almost elusive particle.

Further Reading:

1. A thorough introduction to neutrino oscillation: https://arxiv.org/pdf/1802.05781.pdf
2. Details on mass ordering: https://arxiv.org/pdf/1806.11051.pdf
3. More information about solar neutrinos (from a fellow ParticleBites writer!): https://particlebites.com/?p=6778 
4. A summary of current neutrino experiments and their expected results: https://www.symmetrymagazine.org/article/game-changing-neutrino-experiments 

Print Friendly