November 2019 – ParticleBites

November 28, 2019November 28, 2019

To the Standard Model, and Beyond! with Kaon Decay

Title: “New physics implications of recent search for $K_L \rightarrow \pi^0 \nu \bar{\nu}$ at KOTO”

Author: Kitahara et. al.

Reference: https://arxiv.org/pdf/1909.11111.pdf

The Standard Model, though remarkably accurate in its depiction of many physical processes, is incomplete. There are a few key reasons to think this: most prominently, it fails to account for gravitation, dark matter, and dark energy. There are also a host of more nuanced issues: it is plagued by “fine tuning” problems, whereby its parameters must be tweaked in order to align with observation, and “free parameter” problems, which come about since the model requires the direct insertion of parameters such as masses and charges rather than providing explanations for their values. This strongly points to the existence of as-yet undetected particles and the inevitability of a higher-energy theory. Since gravity should be a theory living at the Planck scale, at which both quantum mechanics and general relativity become relevant, this is to be expected.

A promising strategy for probing physics beyond the Standard Model is to look at decay processes that are incredibly rare in nature, since their small theoretical uncertainties mean that only a few event detections are needed to signal new physics. A primary example of this scenario in action is the discovery of the positron via particle showers in a cloud chamber back in 1932. Since particle physics models of the time predicted zero anti-electron events during these showers, just one observation was enough to herald a new particle.

The KOTO experiment, conducted at the Japan Proton Accelerator Research Complex (J-PARC), takes advantage of this strategy. The experiment was designed specifically to investigate a promising rare decay channel: $K_L \rightarrow \pi^0 \nu \bar{\nu}$ , the decay of a neutral long kaon into a neutral pion, a neutrino, and an antineutrino. Let’s break down this interaction and discuss its significance. The kaon, a meson composed of an up quark and anti-strange quark, comes in both long and short varieties, describing the time of decay relative to each other. The Standard Model predicts a branching ratio of $3 \times 10^{-11}$ for this particular decay process, meaning that out of all the neutral long kaons that decay, only this tiny fraction of them decay into the combination of a neutral pion, neutrino, and an antineutrino, making it incredibly rare for this process to be observed in nature.

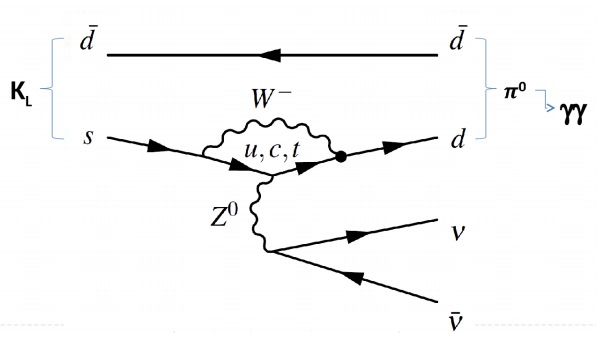
The Feynman diagram describing how a neutral pion, neutrino, and antineutrino are produced from a neutral long kaon. We note the production of two photons, a key observation for the KOTO experiment’s verification of event detection, as this differentiates this process from other neutral long kaon decay channels. Source: https://arxiv.org/pdf/1910.07585.pdf

Here’s where it gets exciting. The KOTO experiment recently reported four signal events within this decay channel where the Standard Model predicts just $0.10 \pm 0.02$ events. If all four of these events are confirmed as the desired neutral long kaon decays, new physics is required to explain the enhanced signal. There are several possibilities, recently explored in a new paper by Kitahara et. al., for what this new physics might be. Before we go into too much detail, let’s consider how KOTO’s observation came to be.

The KOTO experiment is a fixed-target experiment, in which particles are accelerated and collide with something stationary. In this case, protons at energy 30 GeV collided with gold, producing a beam of kaons after other products are diverted with collimators and magnets. The observation of the desired $K_L \rightarrow \pi^0 \nu \bar{\nu}$ mode is particularly difficult experimentally for several reasons. First, the initial and final decay products are neutrally charged, making them harder to detect since they do not ionize, a primary strategy for detecting charged particles. Second, neutral pions are produced via several other kaon decay channels, requiring several strategies to differentiate neutral pions produced by $K_L \rightarrow \pi^0 \nu \bar{\nu}$ from those produced from $K_L \rightarrow 3 \pi^0$ , $K_L \rightarrow 2\pi^0$ , and $K_L \rightarrow \pi^0 \pi^+ \pi^-$ , among others. As we can see in the Feynman diagram above, our desired decay mode has the advantage of producing two photons, allowing KOTO to observe these photons and their transverse momentum in order to pinpoint a $K_L \rightarrow \pi^0 \nu \bar{\nu}$ decay. In terms of experimental construction, KOTO included charged veto detectors in order to reject events with charged particles in the final state and a systematic study of background events was performed in order to discount hadron showers originating from neutrons in the beam line.

This setup was in service of KOTO’s goal to explore the question of CP violation with long kaon decay. CP violation refers to the violation of charge-parity symmetry, the combination of charge-conjugation symmetry (in which a theory is unchanged when we swap a particle for its antiparticle) and parity symmetry (in which a theory is invariant when left and right directions are swapped). We seek to understand why some processes seem to preserve CP symmetry when the Standard Model allows for violation, as is the case in quantum chromodynamics (QCD), and why some processes break CP symmetry, as is seen in the quark mixing matrix (CKM matrix) and the neutrino oscillation matrix. Overall, CP violation has implications for matter-antimatter asymmetry, the question of why the universe seems to be composed predominantly of matter when particle creation and decay processes produce equal amounts of both matter and antimatter. An imbalance of matter and antimatter in the universe could be created if CP violation existed under the extreme conditions of the early universe, mere seconds after the Big Bang. Explanations for matter-antimatter asymmetry that do not involve CP violation generally require the existence of primordial matter-antimatter asymmetry, effectively dodging the fundamental question. The observation of CP violation with KOTO could provide critical evidence toward an eventual answer.

The Kitahara paper provides three interpretations of KOTO’s observation that incorporate physics beyond the Standard Model: new heavy physics, new light physics, and new particle production. The first, new heavy physics, amplifies the expected Standard Model signal via the incorporation of new operators that couple to existing Standard Model particles. If this coupling is suppressed, it could adequately explain the observed boost in the branching ratio. Light new physics involves reinterpreting the neutrino-antineutrino pair as a new light particle. Factoring in experimental constraints, this new light particle should decay in with a finite lifetime on the order of 0.1-0.01 nanoseconds, making it almost completely invisible to experiment. Finally, new particles could be produced within the $K_L \rightarrow \pi^0 \nu \bar{\nu}$ decay channel, which should be light and long-lived in order to allow for its decay to two photons. The details of these new particle scenarios should involve constraints from other particle physics processes, but each serve to increase the branching ratio through direct production of more final state particles. On the whole, this demonstrates the potential for the $K_L \rightarrow \pi^0 \nu \bar{\nu}$ to provide a window to physics beyond the Standard Model.

Of course, this analysis presumes the accuracy of KOTO’s four signal events. Pending the confirmation of these detections, there are several exciting possibilities for physics beyond the Standard Model, so be sure to keep your eye on this experiment!

Learn More:

An overview of the KOTO experiment’s data taking: https://arxiv.org/pdf/1910.07585.pdf
A description of the sensitivity involved in the KOTO experiment’s search: https://j-parc.jp/en/topics/2019/press190304.html
More insights into CP violation: https://www.symmetrymagazine.org/article/charge-parity-violation

November 24, 2019November 24, 2019

Lazy photons at the LHC

Title: “Search for long-lived particles using delayed photons in
proton-proton collisions at √ s = 13 TeV”

Author: CMS Collaboration

Reference: https://arxiv.org/abs/1909.06166 (submitted to Phys. Rev. D)

An interesting group of searches for new physics at the LHC that has been gaining more attention in recent years relies on reconstructing and identifying physics objects that are displaced from the original proton-proton collision point. Several theoretical models predict such signatures due to the decay of long-lived particles (LLPs) that are produced in these collisions. Theories with LLPs typically feature a suppression of the available phase space for the decay of these particles, or a weak coupling between them and Standard Model (SM) particles.

An appealing feature of these signatures is that backgrounds can be greatly reduced by searching for displaced objects, since most SM physics display only prompt particles (i.e. produced immediately following the collision within the primary vertex resolution). Given that the sensitivity to new physics is determined both by the presence of signal events as well as by the absence of background events, the sensitivity to models with LLPs is increased with the expectation of low SM backgrounds.

A recent search for new physics with LLPs performed by the CMS Collaboration uses delayed photons as its driving experimental signature. For this search, events of interest contain delayed photons and missing transverse momentum (MET¹). This signature is predicted in the LHC by various theories such as Gauge-Mediated Supersymmetry Breaking (GMSB), where long-lived supersymmetric particles produced in proton-proton (pp) collisions decay in a peculiar pattern, giving rise to stable particles that escape the detector (hence the MET) and also photons that are displaced from the interaction point. The expected signature is shown in Figure 1.

Figure 1. Example Feynman diagrams of Gauge-Mediated Supersymmetry Breaking (GMSB) processes that can give rise to final-state signatures at CMS consisting of two (left) or one (right) displaced photons and supersymmetric particles that escape the detector and show up as missing transverse momentum (MET) .

The main challenge of this analysis is the physics reconstruction of delayed photons, something that the LHC experiments were not originally designed to do. Both the detector and the physics software are optimized for prompt objects originating from the pp interaction point, where the vast majority of relevant physics happens at the LHC. This difference is illustrated in Figure 2.

Figure 2. Difference between prompt and displaced photons as seen at CMS with the electromagnetic calorimeter (ECAL). The ECAL crystals are oriented towards the interaction point and so for displaced photons both the shape of the electromagnetic shower generated inside the crystals and the arrival time of the photons are different from prompt photons produced at the proton-proton collision. Source: https://cms.cern/news/its-never-too-late-photons-cms

In order to reconstruct delayed photons, a separate reconstruction algorithm was developed that specifically looked for signs of photons out-of-sync with the pp collision. Before this development, out-of-time photons in the detector were considered something of an ‘incomplete or misleading reconstruction’ and discarded from the analysis workflow.

In order to use delayed photons in analysis, a precise understanding of CMS’s calorimeter timing capabilities is required. The collaboration measured the timing resolution of the electromagnetic calorimeter to be around 400 ps, and that sets the detector’s sensitivity to delayed photons.

Other relevant components of this analysis include a dedicated trigger (for 2017 data), developed to select events consistent with a single displaced photon. The identification of a displaced photon at the trigger level relies on the shape of the electromagnetic shower it deposits on the calorimeter: displaced photons produce a more elliptical shower, whereas prompt photons produce a more circular one. In addition, an auxiliary trigger (used for 2016 data, before the special trigger was developed) requires two photons, but no displacement.

The event selection requires one or two well-reconstructed high-momentum photons in the detector (depending on year), and at least 3 jets. The two main kinematic features of the event, the large arrival time (i.e. consistent with time of production delayed relative to the pp collision) and large MET, are used instead to extract the signal and the background yields (see below).

In general for LLP searches, it is difficult to estimate the expected background from Monte Carlo (MC) simulation alone, since a large fraction of backgrounds are due to detector inefficiencies and/or physics events that have poor MC modeling. Instead, this analysis estimates the background from the data itself, by using the so-called ‘ABCD’ method.

The ABCD method consists of placing events in data that pass the signal selection on a 2D histogram, with a suitable choice of two kinematic quantities as the X and Y variables. These two variables must be uncorrelated, a very important assumption. Then this histogram is divided into 4 regions or ‘bins’, and the one with the highest fraction of expected signal events becomes the ‘signal’ bin (call it the ‘C’ bin). The other three bins should contain mostly background events, and with the assumption that X and Y variables are uncorrelated, it is possible to predict the background in C by using the observed backgrounds in A, B, and D:

$C_{\textrm{pred}} = \frac{B_{\textrm{obs}} \times D_{\textrm{obs}}}{A_{\textrm{obs}}}$

Using this data-driven background prediction for the C bin, all that remains is to compare the actual observed yield in C to figure out if there is an excess, which could be attributed to the new physics under investigation:

$\textrm{excess} = C_{\textrm{obs}} - C_{\textrm{pred}}$

As an example, Table 1 shows the number of background events predicted and the number of events in data observed for the 2016 run.

Table 1. Observed yield in data ( $N_{\textrm{obs}}^{\textrm{data}}$ ) and predicted background yields ( $N_{\text{bkg(no C)}}^{\textrm{post-fit}}$ and $N_{\textrm{bkg}}^{\textrm{post-fit}}$ ) in the LHC 2016 run, for all four bins (C is the signal-enriched bin). The observed data is entirely compatible with the predicted background, and no excess is seen.

Table 1. Observed yield in data ( $N_{\textrm{obs}}^{\textrm{data}}$ ) and predicted background yields ( $N_{\text{bkg(no C)}}^{\textrm{post-fit}}$ and $N_{\textrm{bkg}}^{\textrm{post-fit}}$ ) in the LHC 2016 run, for all four bins (C is the signal-enriched bin). The observed data is entirely compatible with the predicted background, and no excess is seen.

Combining all the data, the CMS Collaboration did not find an excess of events over the expected background, which would have suggested evidence of new physics. Using statistical analysis, the collaboration can place upper limits on the possible mass and lifetime of new supersymmetric particles predicted by GMSB, based on the absence of excess events. The final result of this analysis is shown in Figure 3, where a mass of up to 500 GeV for the neutralino particle is excluded for lifetimes of 1 meter (here we measure lifetime in units of length by multiplying by the speed of light: $c\tau$ = 1 meter).

Figure 3. Exclusion plots for the GMSB model, featuring exclusion contours of masses and lifetimes for the lightest supersymmetric particle (the neutralino). At its most sensitive mass region (around lifetimes of 1 meter) the CMS result excludes a mass of under 500 GeV for the neutralino, while for lower masses (100-200 GeV) the lifetime exclusion is quite high at around 100 meters or so.

The mass coverage of this search is higher than the previous search done by the ATLAS Collaboration with run 1 data (i.e. years 2010-2012 only), with a much higher sensitivity to longer lifetimes (up to a factor of 10 depending on the mass). But the ATLAS detector has a longitudinally-segmented calorimeter which allows them to precisely measure the direction of displaced photons, and when they do release their results for this search using run 2 data (2016-2018), it should also feature quite a large gain in sensitivity, potentially overshadowing this CMS result. So stay tuned for this exciting cat-and-mouse game between LHC experiments!

Footnotes

1: Here we use the notation MET instead of $P_T^{\textrm{miss}}$ when referring to missing transverse momentum for typesetting reasons.

November 19, 2019November 19, 2019

CMS catches the top quark running

CMS catches the top quark running

Article : “Running of the top quark mass from proton-proton collisions at √ s = 13 TeV“

Authors: The CMS Collaboration

Reference: https://arxiv.org/abs/1909.09193

When theorists were first developing quantum field theory in the 1940’s they quickly ran into a problem. Some of their calculations kept producing infinities which didn’t make physical sense. After scratching their heads for a while they eventually came up with a procedure known as renormalization to solve the problem. Renormalization neatly hid away the infinities that were plaguing their calculations by absorbing them into the constants (like masses and couplings) in the theory, but it also produced some surprising predictions. Renormalization said that all these ‘constants’ weren’t actually constant at all! The value of these ‘constants’ depended on the energy scale at which you probed the theory.

One of the most famous realizations of this phenomena is the ‘running’ of the strong coupling constant. The value of a coupling encodes the strength of a force. The strong nuclear force, responsible for holding protons and neutrons together, is actually so strong at low energies our normal techniques for calculation don’t work. But in 1973, Gross, Wilczek and Politzer realized that in quantum chromodynamics (QCD), the quantum field theory describing the strong force, renormalization would make the strong coupling constant ‘run’ smaller at high energies. This meant at higher energies one could use normal perturbative techniques to do calculations. This behavior of the strong force is called ‘asymptotic freedom’ and earned them a Nobel prize. Thanks to asymptotic freedom, it is actually much easier for us to understand what QCD predicts for high energy LHC collisions than for the properties of bound states like the proton.

Figure 1: The value of the strong coupling constant (α_s) is plotted as a function of the energy scale. Data from multiple experiments at different energies are compared to the prediction from QCD of how it should run. From [5]

Now for the first time, CMS has measured the running of a new fundamental parameter, the mass of the top quark. More than just being a cool thing to see, measuring how the top quark mass runs tests our understanding of QCD and can also be sensitive to physics beyond the Standard Model. The top quark is the heaviest fundamental particle we know about, and many think that it has a key role to play in solving some puzzles of the Standard Model. In order to measure the top quark mass at different energies, CMS used the fact that the rate of producing a top quark-antiquark pair depends on the mass of the top quark. So by measuring this rate at different energies they can extract the top quark mass at different scales.

Top quarks nearly always decay into W-bosons and b quarks. Like all quarks, the b quarks then create a large shower of particles before they reach the detector called a jet. The W-bosons can decay either into a lepton and a neutrino or two quarks. The CMS detector is very good at reconstructing leptons and jets, but neutrinos escape undetected. However one can infer the presence of neutrinos in an event because we know energy must be conserved in the collision, so if neutrinos are produced we will see ‘missing’ energy in the event. The CMS analyzers looked for top anti-top pairs where one W-boson decayed to an electron and a neutrino and the other decayed to a muon and a neutrino. By using information about the electron, muon, missing energy, and jets in an event, the kinematics of the top and anti-top pair can be reconstructed.

The measured running of the top quark mass is shown in Figure 2. The data agree with the predicted running from QCD at the level of 1.1 sigma, and the no-running hypothesis is excluded at above 95% confidence level. Rather than being limited by the amount of data, the main uncertainties in this result come from the theoretical understanding of the top quark production and decay, which the analyzers need to model very precisely in order to extract the top quark mass. So CMS will need some help from theorists if they want to improve this result in the future.

Figure 2: The ratio of the top quark mass compared to its mass at a reference scale (476 GeV) is plotted as a function of energy. The red line is the theoretical prediction of how the mass should run in QCD.

“The Strengths of Known Forces” https://profmattstrassler.com/articles-and-posts/particle-physics-basics/the-known-forces-of-nature/the-strength-of-the-known-forces/
“Renormalization Made Easy” http://math.ucr.edu/home/baez/renormalization.html
“Studying the Higgs via Top Quark Couplings” https://particlebites.com/?p=4718
“The QCD Running Coupling” https://arxiv.org/abs/1604.08082
CMS Measurement of QCD Running Coupling https://arxiv.org/abs/1609.05331

November 12, 2019November 12, 2019

The lighter side of Dark Matter

Article title: “Absorption of light dark matter in semiconductors”

Authors: Yonit Hochberg, Tongyan Lin, and Kathryn M. Zurek

Reference: arXiv:1608.01994

Direct detection strategies for dark matter (DM) have grown significantly from the dominant narrative of looking for scattering of these ghostly particles off of large and heavy nuclei. Such experiments involve searches for the Weakly-Interacting Massive Particles (WIMPs) in the many GeV (gigaelectronvolt) mass range. Such candidates for DM are predicted by many beyond Standard Model (SM) theories, one of the most popular involving a very special and unique extension called supersymmetry. Once dubbed the “WIMP Miracle”, these types of particles were found to possess just the right properties to be suitable as dark matter. However, as these experiments become more and more sensitive, the null results put a lot of stress on their feasibility.

Typical detectors like that of LUX, XENON, PandaX and ZEPLIN, detect flashes of light (scintillation) from the result of particle collisions in noble liquids like argon or xenon. Other cryogenic-type detectors, used in experiments like CDMS, cool semiconductor arrays down to very low temperatures to search for ionization and phonon (quantized lattice vibration) production in crystals. Already incredibly successful at deriving direct detection limits for heavy dark matter, new ideas are emerging to look into the lighter side.

Recently, DM below the GeV range have become the new target of a huge range of detection methods, utilizing new techniques and functional materials – semiconductors, superconductors and even superfluid helium. In such a situation, recoils from the much lighter electrons in fact become much more sensitive than those of such large and heavy nuclear targets.

There are several ways that one can consider light dark matter interacting with electrons. One popular consideration is to introduce a new gauge boson that has a very small ‘kinetic’ mixing with the ordinary photon of the Standard Model. If massive, these ‘dark photons’ could also be potentially dark matter candidates themselves and an interesting avenue for new physics. The specifics of their interaction with the electron are then determined by the mass of the dark photon and the strength of its mixing with the SM photon.

Typically the gap between the valence and conduction bands in semiconductors like silicon and germanium is around an electronvolt (eV). When the energy of the dark matter particle exceeds the band gap, electron excitations in the material can usually be detected through a complicated secondary cascade of electron-hole pair generation. Below the band gap however, there is not enough energy to excite the electron to the conduction band, and so detection proceeds through low-energy multi-phonon excitations, with the dominant being the emission of two back-to-back phonons.

In both these regimes, the absorption rate of dark matter in the material is directly related to the properties of the material, namely its optical properties. In particular, the absorption rate for ordinary SM photons is determined by the polarization tensor in the medium, and in turn the complex conductivity, $\hat{\sigma}(\omega)=\sigma_{1}+i \sigma_{2}$ , through what is known as the optical theorem. Ultimately this describes the response of the material to an electromagnetic field, which has been measured in several energy ranges. This ties together the astrophysical properties of how the dark matter moves through space and the fundamental description of DM-electron interactions at the particle level.

In a more technical sense, the rate of DM absorption, in events per unit time per unit target mass, is given by the following equation:

$R=\frac{1}{\rho} \frac{\rho_{D M}}{m_{A^{\prime}}} \kappa_{e f f}^{2} \sigma_{1}$

$\rho$ – mass density of the target material
$\rho_{DM}$ – local dark matter mass density (0.3 GeV/cm³) in the galactic halo
$m_{A'}$ – mass of the dark photon particle
$\kappa_{eff}$ – kinetic mixing parameter (in-medium)
$\sigma_1$ – absorption rate of ordinary SM photons

Shown in Figure 1, the projected sensitivity at 90% confidence limit (C.L.) for a 1 kg-year exposure of semiconductor target to dark photon detection can be almost an order of magnitude greater than existing nuclear recoil experiments. Dependence is shown on the kinetic mixing parameter and the mass of the dark photon. Limits are also shown for existing semiconductor experiments, known as DAMIC and CDMSLite with 0.6 and 70 kg-day exposure, respectively.

Figure 1. Projected reach of a silicon (blue, solid) and germanium (green, solid) semiconductor target at 90% C.L. for 1 kg-year exposure through the absorption of dark photons DM, kinetically mixed with SM photons. Multi-phonon excitations are significant for the sub-eV range, and electron excitations approximately over 0.6 and 1 eV (the size of the band gaps for germanium and silicon, respectively).

Furthermore, in the millielectronvolt-kiloelectronvolt range, these could provide much stronger constraints than any of those that currently exist from sources in astrophysics, even at this exposure. These materials also provide a novel way of detecting DM in a single experiment, so long as improvements are made in phonon detection.

These possibilities, amongst a plethora of other detection materials and strategies, can open up a significant area of parameter space for finally closing in on the identity of the ever-elusive dark matter!

References and further reading:

SENSEI searches for light dark matter, https://www.symmetrymagazine.org/article/sensei-searches-for-light-dark-matter
Berkeley leans into search for light dark matter, https://www.symmetrymagazine.org/article/berkeley-leans-into-search-for-light-dark-matter
What if dark matter is lighter? Report calls for small experiments to broaden the hunt, https://www.sciencedaily.com/releases/2019/06/190610090056.htm
Knapen, S., Lin, T., Pyle, M., Zurek, K.M., Detection of light dark matter with optical phonons in polar materials (arXiv:1712.06598)

November 8, 2019November 8, 2019

Discovering the Tau

This plot [1] is the first experimental evidence for the particle that would eventually be named the tau.

On the horizontal axis is the energy of the experiment. This particular experiment collided electron and positron beams. On the vertical axis is the cross section of a specific event resulting from the electron and positron beams colliding. The cross section is like a probability for a given event to occur. When two particles collide, many many things can happen, each with their own probability. The cross section for an event encodes the probability for that particular event to occur. Events with larger probability have larger cross sections and vice versa.

The collaboration found one event could not be explained by the Standard Model at the time. The event in question looks like:

This event is peculiar because the final state contains both an electron and a muon with opposite charges. In 1975, when this paper was published, there was no way to obtain this final state, from any known particles or interactions.

In order to explain this anomaly, particle physicists proposed the following explanations:

Pair production of a heavy lepton. With some insight from the future, we will call this heavy lepton the “tau.”
Pair production of charged Bosons. These charged bosons actually end up being the bosons that mediate the weak nuclear force.

The production of tau’s and these bosons are not equally likely though. Depending on the initial energy of the beams, we are more likely to produce one than the other. It turns out that at the energies of this experiment (a few GeV), it is much more likely to produce taus than to produce the bosons. We would say that the taus have a larger cross section than the bosons. From the plot, we can read off that the production of taus, their cross section, is largest at around 5 GeV of energy. Finally, since these taus are the result of pair production, they are produced in pairs. This bump at 5 GeV is the energy at which it is most likely to produce a pair of taus. This plot then predicts the tau to have a mass of about 2.5 GeV.

References

[1] – Evidence for Anomalous Lepton Production in e+−e− Annihilation. This is the original paper that announced the anomaly that would become the Tau.

[2] – The Discovery of the Tau Lepton. This is a comprehensive story of the discovery of the Tau, written by Martin Perl who would go on to win the 1995 Nobel prize in Physics for its discovery.

[3] – Lepton Review. Hyperphysics provides an accessible review of the Leptonic sector of the Standard Model.

November 1, 2019February 12, 2020

The Early Universe in a Detector: Investigations with Heavy-Ion Experiments

Title: “Probing dense baryon-rich matter with virtual photons”

Author: HADES Collaboration

Reference: https://www.nature.com/articles/s41567-019-0583-8

The quark-gluon plasma, a sea of unbound quarks and gluons moving at relativistic speeds thought to exist at extraordinarily high temperature and density, is a phase of matter critical to our understanding of the early universe and extreme stellar interiors. On the timescale of milliseconds after the Big Bang, the matter in the universe is postulated to have been in a quark-gluon plasma phase, before the universe expanded, cooled, and formed the hadrons we observe today from constituent quarks and gluons. The study of quark matter, the range of phases formed from quarks and gluons, can provide us with insight into the evanescent early universe, providing an intriguing focus for experimentation. Astrophysical objects that are comprised of quarks, such as neutron stars, are also thought to house the necessary conditions for the formation of quark-gluon plasma at their cores. With the accumulation of new data from neutron star mergers, studies of quark matter are becoming increasingly productive and rife for new discovery.

Quantum chromodynamics (QCD) is the theory of quarks and the strong interaction between them. In this theory, quarks and force-carrying gluons, the aptly-named particles that “glue” quarks together, have a “color” charge analogous to charge in quantum electrodynamics (QED). In QCD, the gluon field is often modeled as a narrow tube between two color charges with a constant strong force between them, in contrast with the inverse-square dependence on distance for fields in QED. The pair potential energy between the quarks increases linearly with separation, eventually surpassing the creation energy for a new quark-antiquark pair. Hence, the quarks cannot exist in unbound pairs at low energies, a property known as color confinement. When separation is attempted between quarks, new quarks are instead produced. In particle accelerators, physicists see “jets” of new color-neutral particles (mesons and baryons) in the process of hadronization. At high energies, the story changes and hinges on an idea known as asymptotic freedom, in which the strength of particle interactions decreases with increased energy scale in certain gauge theories such as QCD.

A Feynman diagrammatic scheme of the production of new hadrons from a dilepton collision. We observe an electron-positron pair annihilating to a virtual photon, which then decays to many hadrons via hadronization. Source: https://cds.cern.ch/record/317673

QCD matter is commonly probed with heavy-ion collision experiments and quark-gluon plasma has been produced before in minute quantities at the Relativistic Heavy Ion Collider (RHIC) at Brookhaven National Lab as well as the Large Hadron Collider (LHC) at CERN. The goal of these experiments is to create conditions similar to those of the early universe or at the center of dense stars — doing so requires intense temperatures and an abundance of quarks. Heavy-ions, such as gold or lead nuclei, fit this bill when smashed together at relativistic speeds. When these collisions occur, the resulting “fireball” of quarks and gluons is unstable and quickly decays into a barrage of new, stable hadrons via the hadronization method discussed above.

There are several main goals of heavy-ion collision experiments around the world, revolving around the study of the phase diagram for quark matter. The first component of this is the search for the critical point: the endpoint of the line of first-order phase transitions. The phase transition between hadronic matter, in which quarks and gluons are confined, and partonic matter, in which they are dissociated in a quark-gluon plasma, is also an active area of investigation. There is additionally an ongoing search for chiral symmetry restoration at finite temperature and finite density. A chiral symmetry occurs when the handedness of the particles remains invariant under a parity transformation, that is, when the sign of a spatial coordinate is flipped. However, in QCD, a symmetric system becomes asymmetric in a process known as spontaneous symmetry breaking. Several experiments are designed to investigate evidence of the restoration of this symmetry.

The phase diagram for quark matter, a plot of chemical potential vs. temperature, has many unknown points of interest. Source: https://www.sciencedirect.com/science/article/pii/S055032131630219X

The HADES (High-Acceptance DiElectron Spectrometer) collaboration is a group attempting to address such questions. In a recent experiment, HADES focused on the creation of quark matter via collisions of a beam of Au (gold) ions with a stack of Au foils. Dileptons, which are bound lepton-antilepton pairs that emerge from the decay of virtual particles, are a key element of HADES’ findings. In quantum field theory (QFT), in which particles are modeled as excitations in an underlying field, virtual particles can be thought of as excitations in the field that are transient due to limitations set by the uncertainty principle. Virtual particles are represented by internal lines in Feynman diagrams, are used as tools in calculations, and are not isolated or measured on their own — they are only exchanged with ordinary particles. In the HADES experiment, the virtual photons that produce dileptons which immediately decouple from the strong force. Produced at all stages of QCD interaction, they are ideal messengers of any modification of hadron properties. They are also thought to contain information about the thermal properties of the underlying medium.

To actually extract this information, the HADES detector utilizes a time-of-flight chamber and ring-imaging Cherenkov (RICH) chamber, which identifies particles using the characteristics of Cherenkov radiation: electromagnetic radiation emitted when a particle travels through a dielectric medium at a velocity greater than the phase velocity of light in that particular medium. The detector is then able to measure the invariant mass, rapidity (a commonly-used substitute measure for relativistic velocity), and transverse momentum of emitted electron-positron pairs, the dilepton of choice. In accelerator experiments, there are typically a number of selection criteria in place to ensure that the machinery is detecting the desired particles and the corresponding data is recorded. When a collision event occurs within HADES, a number of checks are in place to ensure that only electron-positron events are kept, factoring in both the number of detected events and detector inefficiency, while excess and background data is thrown out. The end point of this data collection is a calculation of the four-momenta of each lepton pair, a description of its relativistic energy and momentum components. This allows for the construction of a dilepton spectrum: the distribution of the invariant masses of detected dileptons.

The main data takeaway from this experiment was the observation of an excess of dilepton events in an exponential shape, contrasting with the expected number of dileptons from ordinary particle collisions. This suggests a shift in the properties of the underlying matter, with a reconstructed temperature above 70 MeV (note that particle physicists tend to quote temperatures in more convenient units of electron volts). The kicker comes when the group compares these results to simulated neutron star mergers, with expected core temperatures of 75 MeV. This means that the bulk matter created within HADES is similar to the highly dense matter formed in such mergers, a comparison which has become recently accessible due to multi-messenger signals incorporating both electromagnetic and gravitational wave data.

Practically, we see that HADES’ approach is quite promising for future studies of matter under extreme conditions, with the potential to reveal much about the state of the universe early on in its history as well as probe certain astrophysical objects — an exciting realization!