Authors: I. Agullo, A. del Rio and J. Navarro-Salas
Reference: arXiv:1607.08879
Disclaimer: this blogpost requires some basic knowledge of QFT (or being comfortable with taking my word at face value for some of the claims made :))
Anomalies exists everywhere. Probably the most intriguing ones are medical, but in particle physics they can be pretty fascinating too. In physics, anomalies refer to the breaking of a symmetry. There are basically two types of anomalies:
- The first type, gauge anomalies, are red-flags: if they show up in your theory, they indicate that the theory is mathematically inconsistent.
- The second type of anomaly does not signal any problems with the theory and in fact can have experimentally observable consequences. A prime example is the chiral anomaly. This anomaly nicely explains the decay rate of the neutral pion into two photons.

Fig. 1: Illustration of pion decay into two photons. [Credit: Wikimedia Commons]
In this paper, a new anomaly is discussed. This anomaly is related to the polarization of light and is called the electromagnetic duality anomaly.
Chiral anomaly 101
So let’s first brush up on the basics of the chiral anomaly. How does this anomaly explain the decay rate of the neutral pion into two photons? For that we need to start with the Lagrangian for QED that describes the interactions between the electromagnetic field (that is, the photons) and spin-½ fermions (which pions are build from):
$latex \displaystyle \mathcal L = \bar\psi \left( i \gamma^\mu \partial_\mu – i e \gamma^\mu A_\mu \right) \psi + m \bar\psi \psi$
where the important players in the above equation are the $latex \psi$s that describe the spin-½ particles and the vector potential $latex A_\mu$ that describes the electromagnetic field. This Lagrangian is invariant under the chiral symmetry:
$latex \displaystyle \psi \to e^{i \gamma_5} \psi .$
Due to this symmetry the current density $latex j^\mu = \bar{\psi} \gamma_5 \gamma^\mu \psi$ is conserved: $latex \nabla_\mu j^\mu = 0$. This then immediately tells us that the charge associated with this current density is time-independent. Since the chiral charge is time-independent, it prevents the $latex \psi$ fields to decay into the electromagnetic fields, because the $latex \psi$ field has a non-zero chiral charge and the photons have no chiral charge. Hence, if this was the end of the story, a pion would never be able to decay into two photons.
However, the conservation of the charge is only valid classically! As soon as you go from classical field theory to quantum field theory this is no longer true; hence, the name (quantum) anomaly. This can be seen most succinctly using Fujikawa’s observation that even though the field $latex \psi$ and Lagrangian are invariant under the chiral symmetry, this is not enough for the quantum theory to also be invariant. If we take the path integral approach to quantum field theory, it is not just the Lagrangian that needs to be invariant but the entire path integral needs to be:
$latex \displaystyle \int D[A] \, D[\bar\psi]\, \int D[\psi] \, e^{i\int d^4x \mathcal L}$ .
From calculating how the chiral symmetry acts on the measure $latex D \left[\psi \right] \, D \left[\bar \psi \right]$, one can extract all the relevant physics such as the decay rate.
The electromagnetic duality anomaly
Just like the chiral anomaly, the electromagnetic duality anomaly also breaks a symmetry at the quantum level that exists classically. The symmetry that is broken in this case is – as you might have guessed from its name – the electromagnetic duality. This symmetry is a generalization of a symmetry you are already familiar with from source-free electromagnetism. If you write down source-free Maxwell equations, you can just swap the electric and magnetic field and the equations look the same (you just have to send $latex \displaystyle \vec{E} \to \vec{B}$ and $latex \vec{B} \to – \vec{E}$). Now the more general electromagnetic duality referred to here is slightly more difficult to visualize: it is a rotation in the space of the electromagnetic field tensor and its dual. However, its transformation is easy to write down mathematically:
$latex \displaystyle F_{\mu \nu} \to \cos \theta \, F_{\mu \nu} + \sin \theta \, \, ^\ast F_{\mu \nu} .$
In other words, since this is a symmetry, if you plug this transformation into the Lagrangian of electromagnetism, the Lagrangian will not change: it is invariant. Now following the same steps as for the chiral anomaly, we find that the associated current is conserved and its charge is time-independent due to the symmetry. Here, the charge is simply the difference between the number of photons with left helicity and those with right helicity.
Let us continue following the exact same steps as those for the chiral anomaly. The key is to first write electromagnetism in variables analogous to those of the chiral theory. Then you apply Fujikawa’s method and… *drum roll for the anomaly that is approaching*…. Anti-climax: nothing happens, everything seems to be fine. There are no anomalies, nothing!
So why the title of this blog? Well, as soon as you couple the electromagnetic field with a gravitational field, the electromagnetic duality is broken in a deeply quantum way. The number of photon with left helicity and right helicity is no longer conserved when your spacetime is curved.
Physical consequences
Some potentially really cool consequences have to do with the study of light passing by rotating stars, black holes or even rotating clusters. These astrophysical objects do not only gravitationally bend the light, but the optical helicity anomaly tells us that there might be a difference in polarization between lights rays coming from different sides of these objects. This may also have some consequences for the cosmic microwave background radiation, which is ‘picture’ of our universe when it was only 380,000 years old (as compared to the 13.8 billion years it is today!). How big this effect is and whether we will be able to see it in the near future is still an open question.
Further reading
- An introduction to anamolies using only quantum mechanics instead of quantum field theory is “Anomalies for pedestrians” by Barry Holstein
- The beautiful book “Quantum field theory and the Standard Model” by Michael Schwartz has a nice discussion in the later chapters on the chiral anomaly.
- Lecture notes by Adal Bilal for graduate students on anomalies in general can be found here.




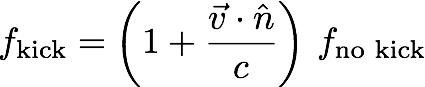

![Fig. 2: If a black hole binary radiates isotropically, it does not experience any kick and the gravitational wave has the black waveform. However, if it experiences a kick along the line of sight, the waveform can get redshifted (when the system moves away from us) as shown on the left of blueshifted (when system moves toward us) as shown on the right. The top and lower panel correspond to the two independent polarizations of the gravitational wave.[Figure taken from this paper]](http://www.particlebites.com/wp-content/uploads/2016/07/figure_redshiftedwave-300x107.jpg)



