When students first learn quantum field theory, the mathematical language the underpins the behavior of elementary particles, they start with the simplest possible interaction you can write down : a particle with no spin and no charge scattering off another copy of itself. One then eventually moves on to the more complicated interactions that describe the behavior of fundamental particles of the Standard Model. They may quickly forget this simplified interaction as a unrealistic toy example, greatly simplified compared to the complexity the real world. Though most interactions that underpin particle physics are indeed quite a bit more complicated, nature does hold a special place for simplicity. This barebones interaction is predicted to occur in exactly one scenario : a Higgs boson scattering off itself. And one of the next big targets for particle physics is to try and observe it.

The Higgs is the only particle without spin in the Standard Model, and the only one that doesn’t carry any type of charge. So even though particles such as gluons can interact with other gluons, its never two of the same kind of gluons (the two interacting gluons will always carry different color charges). The Higgs is the only one that can have this ‘simplest’ form of self-interaction. Prominent theorist Nima Arkani-Hamed has said that the thought of observing this “simplest possible interaction in nature gives [him] goosebumps“.
But more than being interesting for its simplicity, this self-interaction of the Higgs underlies a crucial piece of the Standard Model: the story of how particles got their mass. The Standard Model tells us that the reason all fundamental particles have mass is their interaction with the Higgs field. Every particle’s mass is proportional to the strength of the Higgs field. The fact that particles have any mass at all is tied to the fact that the lowest energy state of the Higgs field is at a non-zero value. According to the Standard Model, early in the universe’s history when the temperature were much higher, the Higgs potential had a different shape, with its lowest energy state at field value of zero. At this point all the particles we know about were massless. As the universe cooled the shape of the Higgs potential morphed into a ‘wine bottle’ shape, and the Higgs field moved into the new minimum at non-zero value where it sits today. The symmetry of the initial state, in which the Higgs was at the center of its potential, was ‘spontaneously broken’ as its new minimum, at a location away from the center, breaks the rotation symmetry of the potential. Spontaneous symmetry breaking is a very deep theoretical idea that shows up not just in particle physics but in exotic phases of matter as well (eg superconductors).
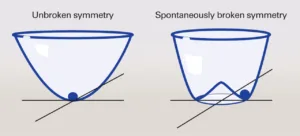
This fantastical story of how particle’s gained their masses, one of the crown jewels of the Standard Model, has not yet been confirmed experimentally. So far we have studied the Higgs’s interactions with other particles, and started to confirm the story that it couples to particles in proportion to their mass. But to confirm this story of symmetry breaking we will to need to study the shape of the Higgs’s potential, which we can probe only through its self-interactions. Many theories of physics beyond the Standard Model, particularly those that attempt explain how the universe ended up with so much matter and very little anti-matter, predict modifications to the shape of this potential, further strengthening the importance of this measurement.
Unfortunately observing the Higgs interacting with itself and thus measuring the shape of its potential will be no easy feat. The key way to observe the Higgs’s self-interaction is to look for a single Higgs boson splitting into two. Unfortunately in the Standard Model additional processes that can produce two Higgs bosons quantum mechanically interfere with the Higgs self interaction process which produces two Higgs bosons, leading to a reduced production rate. It is expected that a Higgs boson scattering off itself occurs around 1000 times less often than the already rare processes which produce a single Higgs boson. A few years ago it was projected that by the end of the LHC’s run (with 20 times more data collected than is available today), we may barely be able to observe the Higgs’s self-interaction by combining data from both the major experiments at the LHC (ATLAS and CMS).
Fortunately, thanks to sophisticated new data analysis techniques, LHC experimentalists are currently significantly outpacing the projected sensitivity. In particular, powerful new machine learning methods have allowed physicists to cut away background events mimicking the di-Higgs signal much more than was previously thought possible. Because each of the two Higgs bosons can decay in a variety of ways, the best sensitivity will be obtained by combining multiple different ‘channels’ targeting different decay modes. It is therefore going to take a village of experimentalists each working hard to improve the sensitivity in various different channels to produce the final measurement. However with the current data set, the sensitivity is still a factor of a few away from the Standard Model prediction. Any signs of this process are only expected to come after the LHC gets an upgrade to its collision rate a few years from now.

While experimentalists will work as hard as they can to study this process at the LHC, to perform a precision measurement of it, and really confirm the ‘wine bottle’ shape of the potential, its likely a new collider will be needed. Studying this process in detail is one of the main motivations to build a new high energy collider, with the current leading candidates being an even bigger proton-proton collider to succeed the LHC or a new type of high energy muon collider.

The quest to study nature’s simplest interaction will likely span several decades. But this long journey gives particle physicists a roadmap for the future, and a treasure worth traveling great lengths for.
Read More:
CERN Courier Interview with Nima Arkani-Hamed on the future of Particle Physics on the importance of the Higgs’s self-coupling
Wikipedia Article and Lecture Notes on Spontaneous symmetry breaking
Recent ATLAS Measurements of the Higgs Self Coupling







