Posted on

Are you smarter than an ATLAS algorithm?

Article: ‘That looks weird’ — evaluating citizen scientists’ ability to detect
unusual features in ATLAS images of LHC collisions
Authors:  A.J. Barra, A. Haasb, C.W. Kalderon
Reference: arXiv:1610.02214v1

As it turns out, non-expert citizen scientists can match or beat out ATLAS algorithms in identifying features in images of LHC collisions.

The ability of the general public to identify long-lived particles and other unusual features in images of LHC collisions recorded by the ATLAS experiment was studied using data from the Higgs Hunters project. The Higgs Hunters project was launched by NYU scientists and colleagues in 2014, and allows members of the general public to study LHC images to help search for previously unobserved particles. Writing computer algorithms to identify “weird looking things” in these images can be difficult, and human eyes, be they expert or non-expert, can help with the hunt. The Higgs Hunters project scientists are specifically searching for previously unobserved particles that could be created via decay of the Higgs. In some cases, the tracks left in the ATLAS experiment could be picked out better by human eyes than computer programs.

This isn’t the first time the scientific community has reached out to non-experts to classify images or aid in scientific pursuits. Through the Galaxy Zoo project, for example, citizen scientists contributed to the results of 48 scientific papers by classifying galaxy shapes and spotting unusual objects in images from the Sloan Digital Sky Survey and other image datasets. In a more indirect way, the public has also been previously invited to contribute to CERN’s science by donating their personal computer’s idle time to help simulate proton-proton collisions. The Higgs Hunters project builds on this history by being the first to allow the general public to take an active role in searching for new particles at the LHC, which not only has the practical benefit of helping scientists out in their search, but also inspires the non-scientist public to take an interest in the field of particle physics.

The task selected for the Higgs Hunters project was that of identifying new particles, \phi, dubbed “baby bosons,” as they decay within the ATLAS detector. Such particles are predicted in theories in which an additional scalar mixes weakly with the Higgs boson. These processes were chosen because they had not been previously unobserved and would generate a signature that is fairly easily identifiable by eye, rendering the citizen scientists competitive with standard reconstruction algorithms. The discovery of these particles would be a high impact scientific discovery, a key motivating feature when employing citizen scientists.

Before being presented to volunteers, images were pre-selected to include those containing a muon and an antimuon with invariant mass consistent with the mass of the Z boson. Such events are consistent with the Z boson decay processes Z \rightarrow \mu^+ + \mu^- and have an increased probability of also containing a Higgs boson, since virtual Z bosons may emit Higgs bosons through the ‘Higgs-strahlung’ process, Z^* \rightarrow Z+H. Data were selected from the 2012 data-taking period between April and December. The ability of the volunteers to identify the desired events was calibrated using test images which showed Monte Carlo simulations of the process of interest, H \rightarrow \phi + \phi. All of the images presented to volunteers, be they simulations or real data, were processed using the ATLAS reconstruction software.

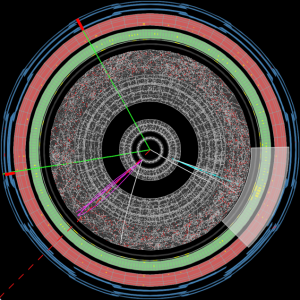
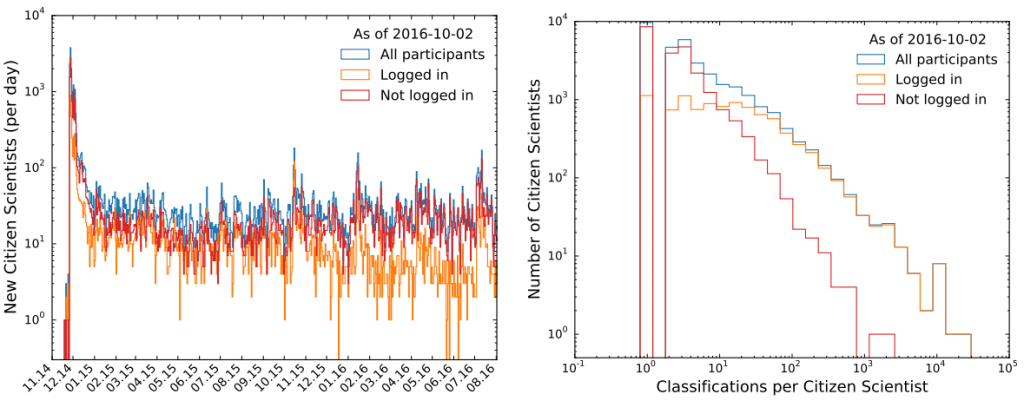
An example ATLAS detector image presented to citizen scientists, generated from a computer simulation of the process H → φ+φ. The green lines emanating from the center indicate the reconstructed muon and antimuon used to select the event. The red dotted line indicates the direction of missing momentum transverse to the beam. Source: arXiv:1610.02214v1

As of October 2016, classifications had been performed by ~32,000 citizen scientists of a wide arrange of ages and backgrounds from 179 countries. Peaks in volunteer activity occurred soon after the project launch and when CERN news stories were published about the project. Each image was classified by ~60 people. The number of classifications completed by each citizen scientist follows an approximate power-law behavior, with most volunteers classifying just a handful of images, but ~1,000 people providing 100+ classifications each. The most dedicated enthusiast provided nearly 20,000 classifications. In total, 1,200,000 features of interest were classified on ~39,000 distinct images.

Left: Start date of new citizen scientists joining the project for the first time. Right: Number of classifications per citizen scientist, displaying an approximate power-law behavior. Source: arXiv:1610.02214v1

It was found that the citizen scientists’ performance competed very well with that of the computer algorithm, even beating it for events with low mass (8 GeV) baby bosons regardless of image view and boson lifetime value. As the mass of the boson increased, the algorithm began beating out the human volunteers. A “weird thing” was also spotted: an image showing a collision apparently containing a jet of multiple collimated muons. In the Standard Model, jets are always of hadrons, not muons. After further investigation by the science team, it was found that the event was due to an unusual interaction of a known particle with the detector, rather than an unusual or new particle. While this didn’t represent a discovery of new physics, the potential of citizen scientists to pick out “weird stuff” could lead to the future identification of interesting features in LHC collision data.

The volunteers responded positively to the project, with the overwhelming majority (>97%) interested in continuing their participation in a future CERN physics project. 47% of respondents said they were more likely to go on to study physics as a result of participating in the project, and 80% felt that their knowledge of particle physics had been improved.

In the future, relying on non-expert citizen scientists could help scientific collaborations classify data as well or better than computer algorithms could, while engaging the public in physics in a valuable and influential way. Just last month, LIGO launched its “Gravity Spy” citizen science program, in which participants search LIGO data for “glitches” that can help LIGO scientists distinguish between the signals they observe.

Background reading:

Posted on

Studying the Higgs via Top Quark Couplings

Article: “Implications of CP-violating Top-Higgs Couplings at LHC and Higgs Factories”

Authors: Archil Kobakhidze, Ning Liu, Lei Wu, and Jason Yue

Reference: arXiv hep-ph 1610.06676

 

It has been nearly five years since scientists at the LHC first observed a new particle that looked a whole lot like the highly sought after Higgs boson. In those five years, they have poked and prodded at every possible feature of that particle, trying to determine its identity once and for all. The conclusions? If this thing is an imposter, it’s doing an incredible job.

This new particle of ours really does seem to be the classic Standard Model Higgs. It is a neutral scalar, with a mass of about 125 GeV. All of its couplings with other SM particles are lying within uncertainty of their expected values, which is very important. You’ve maybe heard people say that the Higgs gives particles mass. This qualitative statement translates into an expectation that the Higgs coupling to a given particle is proportional to that particle’s mass. So probing the values of these couplings is a crucial task.

Figure 1: Best-fit results for the production signal strengths for the combination of ATLAS and CMS. Also shown for completeness are the results for each experiment. The error bars indicate the 1σ intervals.

Figure 1 shows the combined experimental measurements between ATLAS and CMS of Higgs decay signal strengths as a ratio of measurement to SM expectation. Values close to 1 means that experiment is matching theory. Looking at this plot, you might notice that a few of these values have significant deviations from 1, where our perfect Standard Model world is living. Specifically, the ttH signal strength is running a bit high. ttH is the production of a top pair and a Higgs from a single proton collision. There are many ways to do this, starting from the primary Higgs production mechanism of gluon-gluon fusion. Figure 2 shows some example diagrams that can produce this interesting ttH signature. While the deviations are a sign to physicists that maybe we don’t understand the whole picture.

Figure 2: Parton level Feynman diagrams of ttH at leading order.

Putting this in context with everything else we know about the Higgs, that top coupling is actually a key player in the Standard Model game. There is a popular unsolved mystery in the SM called the hierarchy problem. The way we understand the top quark contribution to the Higgs mass, we shouldn’t be able to get such a light Higgs, or a stable vacuum. Additionally, electroweak baryogenesis reveals that there are things about the top quark that we don’t know about.

Now that we know we want to study top-Higgs couplings, we need a way to characterize them. In the Standard Model, the coupling is purely scalar. However, in beyond the SM models, there can also be a pseudoscalar component, which violates charge-parity (CP) symmetry. Figure 3 shows a generic form for the term, where Cst is the scalar and Cpt is the pseudoscalar contribution. What we don’t know right away are the relative magnitudes of these two components. In the Standard Model, Cst = 1 and Cpt = 0. But theory suggests that there may be some non-zero value for Cpt, and that’s what we want to figure out.

Figure 3

Using simulations along with the datasets from Run 1 and Run 2 of the LHC, the authors of this paper investigated the possible values of Cst and Cpt. Figure 4 shows the updated bound. You can see from the yellow 2σ contour that the new limits on the values are |Cpt| < 0.37 and 0.85 < Cst < 1.20, extending the exclusions from Run 1 data alone. Additionally, the authors claim that the cross section of ttH can be enhanced up to 1.41 times the SM prediction. This enhancement could either come from a scenario where Cpt = 0 and Cst > 1, or the existence of a non-zero Cpt component.

Figure 4: The signal strength µtth at 13 TeV LHC on the plane of Cst and Cpt. The yellow contour corresponds to a 2σ limit.

Further probing of these couplings could come from the HL-LHC, through further studies like this one. However, examining the tH coupling in a future lepton collider would also provide valuable insights. The process e+e- à hZ contains a top quark loop. Thus one could make a precision measurement of this rate, simultaneously providing a handle on the tH coupling.

 

References and Further Reading:

  1. “Enhanced Higgs associated production with a top quark pair in the NMSSM with light singlets”. arXiv hep-ph 02353
  2. “Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at √s = 7 and 8 TeV.” ATLAS-CONF-2015-044

 

 

Posted on

The end of the Universe?

Hello nibblers,

Don’t worry, my title doesn’t refer to the recent US election. Only to the end of the Universe due to the Higgs boson. Let me explain…

Last time I wrote, I discussed new methods for determining whether the Higgs boson interacts with itself. As you will recall, establishing whether this is the case is crucial for determining the precise form of the Higgs scalar potential which is responsible for breaking electroweak symmetry and generating masses for the W and Z bosons via the Higgs mechanism. You might also remember that I briefly mentioned that these Higgs self interactions might have deep implications for the stability of our universe. Since I think this topic is interesting enough for its own post I wanted to go into a little more. Its a fascinating topic, but the details can get hairy pretty quickly so ill keep it as simple as possible and just try and give a flavor before going into more detail in future posts.

In the Standard Model, the Higgs potential determines the ‘vacuum’ of our universe, which by definition is the lowest energy state and presumably the one in which we live in today. We can think of the Higgs potential as a ‘background, along with spacetime, in which the various processes which occur in the Universe are acted out. In the Standard Model the Higgs potential before electroweak symmetry can be written as a very simple polynomial in H (after requiring gauge invariance and renormalizability),

V(H) = \mu^2 H^2 + \lambda H^4.

Assuming \mu^2 > 0 and \lambda > 0, this looks like the function drawn in Figure 1. Visually it is easy to see that H = 0 is a minimum of V(H). We call this a stable minimum because if you imagine a ball sitting at the bottom of the ‘bowl’ and moving it to the left or right it will simply role back down to H = 0. Since at this point the energy is a minimum, we call it the vacuum. In order for our universe to be stable we must live in a minimum such as this, i.e. a stable vacuum.

Figure 1: The Higgs potential for $latex \mu^2 > 0$ and $latex \lambda > 0$. This potential has a stable minimum at $latex H = 0$.
Figure 1: The Higgs potential for \mu^2 > 0 and \lambda > 0. This potential has a stable minimum at H = 0.

If on the other hand we have \mu^2 > 0 and \lambda < 0, the potential now looks like that in Figure 2. Clearly now H=0 is no longer a stable point as can be understood by again considering a ball sitting at H = 0 and moving it to the left or right. As we see in Figure 2, instead of rolling back to H = 0 as before, it will simply keep rolling down to the left or right to arbitrarily large values of H, never to return to H = 0. We say this potential is unstable and something like it would be disastrous for our universe. So we see in this very simple example already how the sign of \lambda is crucial for determining whether the vacuum, and as a consequence our universe, is stable.

 

Figure 2: The Higgs potential for $latex \mu^2 > 0$ and $latex \lambda < 0$. This potential is not stable.
Figure 2: The Higgs potential for \mu^2 > 0 and \lambda < 0. This potential is not stable.

Once electroweak symmetry breaking occurs the potential becomes a little more complicated, but more interesting. Still, the stability of our vacuum will depend on the sign of \lambda. We can see this by considering the case \mu^2 < 0 and \lambda > 0 for which the Higgs develops a vacuum expectation value (VEV) and breaks electroweak symmetry. The Higgs potential looks like what we see in Figure 3. Now the minimum is not at H = 0, but at H = \pm v where v is the value of the Higgs’ VEV and we can think of the two minima as equivalent due to symmetry.

Figure 3: The Higgs potential for $latex \mu^2 0$. This potential breaks electroweak symmetry and has a stable minimum at $latex H = v$.
Figure 3: The Higgs potential for \mu^2 < 0 and \lambda > 0. This potential breaks electroweak symmetry and has a stable minimum at H = v.

The subtlety comes when we consider what happens at very large H. In Figure 3 the potential appears to increase forever as H gets larger and thus H = v would an absolute minimum of V(H). But is it possible that at large enough values of H we’ll find another even deeper minimum which would thus be the `true’ vacuum? This is possible if \lambda < 0 which could generate a potential of the form shown in Figure 4.

Figure 4: The Higgs potential for $latex \mu^2 0$. This potential breaks electroweak symmetry and has a 'false' vacuum at $latex H = v$ with the 'true' deeper vacuum at much larger $latex H$.
Figure 4: The Higgs potential for \mu^2 < 0 and \lambda < 0. This potential breaks electroweak symmetry and has a ‘false’ vacuum at H = v with the ‘true’ deeper vacuum at much larger H.

In this case there can be a deeper ‘well’ than the one where we currently live near H = v. Naively we would need enough energy to get over the large humps and fall to the deeper minimum. Thus there is no worry that our Universe will suddenly decay away to some other lowest energy state which probably would not include people and we can rest easy….buuut…this is only what would happen in a classical world.

Here the magic of quantum mechanics (or should I say terror?) comes into play. Due to quantum fluctuations even though the Higgs lives the vast majority of the time in the minimum around H = v there is a tiny probability that the Higgs boson can suddenly fluctuate to very large values of H. If there is a deeper minimum at these large values as shown in Figure 4, then we could quantum mechanically ‘tunnel’ from our current vacuum, to the deeper ‘true’ vacuum.

Needless to say this sounds bad. So what happens in the Standard Model, is the Universe stable? The answer turns out to be closely related to the Higgs boson and top quark masses and takes us into the deep waters of renormalization, but i’ll save this interesting connection to a future post. For now we can just appreciate the importance of determining \lambda by measuring the Higgs self interactions at the LHC or future colliders.

Further reading: 

  1. If you want to start learning about the conept of a vacuum here is a good place to start.
  2. Here again is a basic introduction to the physics of the Standard Model Higgs boson.