Posted on

LHC Run II: What To Look Out For

The Large Hadron Collider is the world’s largest proton collider, and in a mere five years of active data acquisition, it has already achieved fame for the discovery of the elusive Higgs Boson in 2012. Though the LHC is currently off to allow for a series of repairs and upgrades, it is scheduled to begin running again within the month, this time with a proton collision energy of 13 TeV. This is nearly double the previous run energy of 8 TeV,  opening the door to a host of new particle productions and processes. Many physicists are keeping their fingers crossed that another big discovery is right around the corner. Here are a few specific things that will be important in Run II.

 

1. Luminosity scaling

Though this is a very general category, it is a huge component of the Run II excitement. This is simply due to the scaling of luminosity with collision energy, which gives a remarkable increase in discovery potential for the energy increase.

If you’re not familiar, luminosity is the number of events per unit time and cross sectional area. Integrated luminosity sums this instantaneous value over time, giving a metric in the units of 1/area.

lumi                          intLumi

 In the particle physics world, luminosities are measured in inverse femtobarns, where 1 fb-1 = 1/(10-43 m2). Each of the two main detectors at CERN, ATLAS and CMS, collected 30 fb-1 by the end of 2012. The main point is that more luminosity means more events in which to search for new physics.

Figure 1 shows the ratios of LHC luminosities for 7 vs. 8 TeV, and again for 13 vs. 8 TeV. Since the plot is in log scale on the y axis, it’s easy to tell that 13 to 8 TeV is a very large ratio. In fact, 100 fb-1 at 8 TeV is the equivalent of 1 fb-1 at 13 TeV. So increasing the energy by a factor less than 2 increase the integrated luminosity by a factor of 100! This means that even in the first few months of running at 13 TeV, there will be a huge amount of data available for analysis, leading to the likely release of many analyses shortly after the beginning of data acquisition.

lumiRatio
Figure 1: Parton luminosity ratios, from J. Stirling at Imperial College London (see references.)

 

2. Supersymmetry

Supersymmetry theory proposes the existence of a superpartner for every particle in the Standard Model, effectively doubling the number of fundamental particles in the universe. This helps to answer many questions in particle physics, namely the question of where the particle masses came from, known as the ‘hierarchy’ problem (see the further reading list for some good explanations.)

Current mass limits on many supersymmetric particles are getting pretty high, concerning some physicists about the feasibility of finding evidence for SUSY. Many of these particles have already been excluded for masses below the order of a TeV, making it very difficult to create them with the LHC as is. While there is talk of another LHC upgrade to achieve energies even higher than 14 TeV, for now the SUSY searches will have to make use of the energy that is available.

SUSYxsec
Figure 2: Cross sections for the case of equal degenerate squark and gluino masses as a function of mass at √s = 13 TeV, from 1407.5066. q stands for quark, g stands for gluino, and t stands for stop.

 

Figure 2 shows the cross sections for various supersymmetric particle pair production, including squark (the supersymmetric top quark) and gluino (the supersymmetric gluon). Given the luminosity scaling described previously, these cross sections tell us that with only 1 fb-1, physicists will be able to surpass the existing sensitivity for these supersymmetric processes. As a result, there will be a rush of searches being performed in a very short time after the run begins.

 

3. Dark Matter

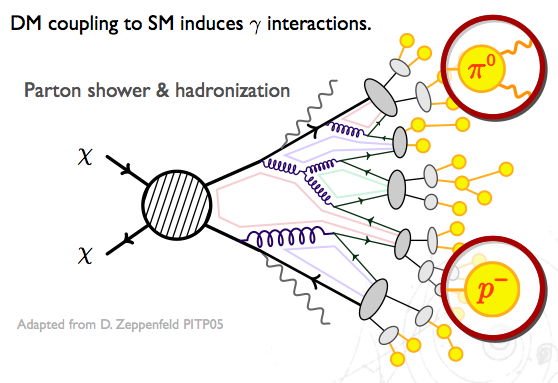
Dark matter is one of the greatest mysteries in particle physics to date (see past particlebites posts for more information). It is also one of the most difficult mysteries to solve, since dark matter candidate particles are by definition very weakly interacting. In the LHC, potential dark matter creation is detected as missing transverse energy (MET) in the detector, since the particles do not leave tracks or deposit energy.

One of the best ways to ‘see’ dark matter at the LHC is in signatures with mono-jet or photon signatures; these are jets/photons that do not occur in pairs, but rather occur singly as a result of radiation. Typically these signatures have very high transverse momentum (pT) jets, giving a good primary vertex, and large amounts of MET, making them easier to observe. Figure 3 shows a Feynman diagram of such a decay, with the MET recoiling off a jet or a photon.

feynmanMonoX
Figure 3: Feynman diagram of mono-X searches for dark matter, from “Hunting for the Invisible.”

 

Though the topics in this post will certainly be popular in the next few years at the LHC, they do not even begin to span the huge volume of physics analyses that we can expect to see emerging from Run II data. The next year alone has the potential to be a groundbreaking one, so stay tuned!

 

References: 

Further Reading:

 

 

Posted on

An update from AMS-02, the particle detector in space

Last Thursday, Nobel Laureate Sam Ting presented the latest results (CERN press release) from the Alpha Magnetic Spectrometer (AMS-02) experiment, a particle detector attached to the International Space Station—think “ATLAS/CMS in space.” Instead of beams of protons, the AMS detector examines cosmic rays in search of signatures of new physics such as the products of dark matter annihilation in our galaxy.

from http://ams.nasa.gov/images_AMS_On-Orbit.html
Image of AMS-02 on the space station, from NASA.

In fact, this is just the latest chapter in an ongoing mystery involving the energy spectrum of cosmic positrons. Recall that positrons are the antimatter versions of electrons with identical properties except having opposite charge. They’re produced from known astrophysical processes when high-energy cosmic rays (mostly protons) crash into interstellar gas—in this case they’re known as `secondaries’ because they’re a product of the `primary’ cosmic rays.

The dynamics of charged particles in the galaxy are difficult to simulate due to the presence of intense and complicated magnetic fields. However, the diffusion models generically predict that the positron fraction—the number of positrons divided by the total number of positrons and electrons—decreases with energy. (This ratio of fluxes is a nice quantity because some astrophysical uncertainties cancel.)

This prediction, however, is in stark contrast with the observed positron fraction from recent satellite experiments:

AMS-02, from http://physics.aps.org/articles/v6/40
Observed positron fraction from recent experiments compared to expected astrophysical background (gray) from APS viewpoint article based on the 2013 AMS-02 results (data) and the analysis in 1002.1910 (background).

The rising fraction had been hinted in balloon-based experiments for several decades, but the satellite experiments have been able to demonstrate this behavior conclusively because they can access higher energies. In their first set of results last year (shown above), AMS gave the most precise measurements of the positron fraction as far as 350 GeV. Yesterday’s announcement extended these results to 500 GeV and added the following observations:

First they claim that they have measured the maximum of the positron fraction to be 275 GeV. This is close to the edge of the data they’re releasing, but the plot of the positron fraction slope is slightly more convincing:

From Phys. Rev. Lett. 113, 121101
Lower: the latest positron fraction data from AMS-02 against a phenomenological model. Upper: slope of the lower curve. From Phys. Rev. Lett. 113, 121101. [Non-paywall summary.]
The observation of a maximum in what was otherwise a fairly featureless rising curve is key for interpretations of the excess, as we discuss below. A second observation is a bit more curious: while neither the electron nor the positron spectra follow a simple power law, \Phi_{e^\pm} \sim E^{-\delta}, the total electron or positron flux does follow such a power law over a range of energies.

...
Total electron/positron flux weighted by the cubed energy and the fit to a simple power law. From the AMS press summary.

This is a little harder to interpret since the flux form electrons also, in principle, includes different sources of background. Note that this plot reaches higher energies than the positron fraction—part of the reason for this is that it is more difficult to distinguish between electrons and positrons at high energies. This is because the identification depends on how the particle bends in the AMS magnetic field and higher energy particles bend less. This, incidentally, is also why the FERMI data has much larger error bars in the first plot above—FERMI doesn’t have its own magnetic field and must rely on that of the Earth for charge discrimination.

So what should one make of the latest results?

The most optimistic hope is that this is a signal of dark matter, and at this point this is more of a ‘wish’ than a deduction. Independently of AMS, we know is that dark matter exists in a halo that surrounds our galaxy. The simplest dark matter models also assume that when two dark matter particles find each other in this halo, they can annihilate into Standard Model particle–anti-particle pairs, such as electrons and positrons—the latter potentially yielding the rising positron fraction signal seen by AMS.

From a particle physics perspective, this would be the most exciting possibility. The ‘smoking gun’ signature of such a scenario would be a steep drop in the positron fraction at the mass of the dark matter particle. This is because the annihilation occurs at low velocities so that the energy of the annihilation products is set by the dark matter mass. This is why the observation of a maximum in the positron fraction is interesting: the dark matter interpretation of this excess hinges on how steeply the fraction drops off.

There are, however, reasons to be skeptical.

  • One attractive feature of dark matter annihilations is thermal freeze out: the observation that the annihilation rate determines how much dark matter exists today after being in thermal equilibrium in the early universe. The AMS excess is suggestive of heavy (~TeV scale) dark matter with an annihilation rate three orders of magnitude larger than the rate required for thermal freeze out.
  • A study of the types of spectra one expects from dark matter annihilation shows fits that are somewhat in conflict with the combined observations of the positron fraction, total electron/positron flux, and the anti-proton flux (see 0809.2409). The anti-proton flux, in particular, does not have any known excess that would otherwise be predicted by dark matter annihilation into quarks.

There are ways around these issues, such as invoking mechanisms to enhance the present day annihilation rate, perhaps with the annihilation only creating leptons and not quarks. However, these are additional bells and whistles that model-builders must impose on the dark matter sector. It is also important to consider alternate explanations of the Pamela/FERMI/AMS positron fraction excess due to astrophysical phenomena. There are at least two very plausible candidates:

  1. Pulsars are neutron stars that are known to emit “primary” electron/positron pairs. A nearby pulsar may be responsible for the observed rising positron fraction. See 1304.1791 for a recent discussion.
  2. Alternately, supernova remnants may also generate a “secondary” spectrum of positrons from acceleration along shock waves (0909.4060, 0903.2794, 1402.0855).

Both of these scenarios are plausible and should temper the optimism that the rising positron fraction represents a measurement of dark matter. One useful handle to disfavor the astrophysical interpretations is to note that they would be anisotropic (not constant over all directions) whereas the dark matter signal would be isotropic. See 1405.4884 for a recent discussion. At the moment, the AMS measurements do not measure any anisotropy but are not yet sensitive enough to rule out astrophysical interpretations.

Finally, let us also point out an alternate approach to understand the positron fraction. The reason why it’s so difficult to study cosmic rays is that the complex magnetic fields in the galaxy are intractable to measure and, hence, make the trajectory of charged particles hopeless to trace backwards to their sources. Instead, the authors of 0907.1686 and 1305.1324 take an alternate approach: while we can’t determine the cosmic ray origins, we can look at the behavior of heavier cosmic ray particles and compare them to the positrons. This is because, as mentioned above, the bending of a charged particle in a magnetic field is determined by its mass and charge—quantities that are known for the various cosmic ray particles. Based on this, the authors are able to predict an upper bound for the positron fraction when one assumes that the positrons are secondaries (e.g in the case of supernovae  remnant acceleration):

from arXiv:1305.1324 , see Resonaances for an update
Upper bound on secondary positron fraction from 1305.1324. See Resonaances for an updated plot with last week’s data.

We see that the AMS-02 spectrum is just under the authors’ upper bound, and that the reported downturn is consistent with (even predicted from) the upper-bound. The authors’ analysis then suggests a non-dark matter explanation for the positron excess. See this post from Resonaances for a discussion of this point and an updated version of the above plot from the authors.

With that in mind, there are at least three things to look forward to in the future from AMS:

  1. A corresponding upturn in the anti-proton flux is predicted in many types of dark matter annihilation models for the rising positron fraction. Thus far AMS-02 has not released anti-proton data due to the lower numbers of anti-protons.
  2. Further sensitivity to the (an)isotropy of the excess is a critical test of the dark matter interpretation.
  3. The shape of the drop-off with energy is also critical: a gradual drop-off is unlikely to come from dark matter whereas a steep drop off is considered to be a smoking gun for dark matter.

Only time will tell; though Ting suggested that new results would be presented at the upcoming AMS meeting at CERN in 2 months.

 

Further reading:

This post was edited by Christine Muccianti. 

Posted on

New Results from the CRESST-II Dark Matter Experiment

  • Title: Results on low mass WIMPs using an upgraded CRESST-II detector
  • Author: G. Angloher, A. Bento, C. Bucci, L. Canonica, A. Erb, F. v. Feilitzsch, N. Ferreiro Iachellini, P. Gorla, A. Gütlein, D. Hauff, P. Huff, J. Jochum, M. Kiefer, C. Kister, H. Kluck, H. Kraus,  J.-C. Lanfranchi, J. Loebell, A. Münster, F. Petricca, W. Potzel, F. Pröbst, F. Reindl, S. Roth, K. Rottler, C. Sailer, K. Schäffner, J. Schieck, J. Schmaler, S. Scholl, S. Schönert, W. Seidel, M. v. Sivers, L. Stodolsky, C. Strandhagen, R. Strauss, A. Tanzke, M. Uffinger, A. Ulrich, I. Usherov, M. Wüstrich, S. Wawoczny, M. Willers, and A. Zöller
  • Published: arXiv:1407.3146 [astro-ph.CO]

CRESST-II (Cryogenic Rare Event Search with Superconducting Thermometers) is a dark matter search experiment located at the Laboratori Nazionali del Gran Sasson in Italy. It is primarily involved with the search for WIMPs, or Weakly Interacting Massive Particles, which play a key role in both particle and astrophysics as a potential candidate for dark matter. If you are not yet intrigued enough about dark matter, see the list of references at the bottom of this post for more information. As dark matter candidates, WIMPs only interact via gravitational and weak forces, making them extremely difficult to detect.

CRESST-II attempts to detect WIMPs via elastic scattering off nuclei in scintillating CaWO4 crystals. This is a process known as direct detection, where scientists search for evidence of the WIMP itself; indirect detection requires searching for WIMP decay products. There are many challenges to direct detection, including the relatively low amount of recoil energy present in such scattering. An additional issue is the extremely high background, which is dominated by beta and gamma radiation of the nuclei. Overall, the experiment expects to obtain a few tens of events per kilogram-year.

CRESST1
Figure 1: Expected number of events for background and signal in 2011 CRESST-II run; from 1109.0702v1.

 

In 2011, CREST-II reported a small excess of events outside of the predicted background levels. The statistical analysis makes use of a maximum likelihood function, which parameterizes each primary background to compute a total number of expected events. The results of this likelihood fit can be seen in Figure 1, where M1 and M2 are different mass hypotheses. From these values, CRESST-II reports a statistical significance of 4.7σ for M1, and 4.2σ for M2. Since a discovery is generally accepted to have a significance of 5σ, these numbers presented a pretty big cause for excitement.

 

 

 

In July of 2014, CRESST-II released a follow up paper: after some detector upgrades and further background reduction, these tantalizingly high significances have been revised, ruling out both mass hypotheses. The event excess was likely due to unidentified  e–/γ background, which was reduced by a factor of 2 -10 via improved CaWO4 crystals used in this run. The elimination of these high signal significances is in agreement with other dark matter searches, which have also ruled out WIMP masses on the order of 20 GeV.

Figure 2 shows the most recent exclusion curve for the WIMP mass, which gives the cross section for production as a function of possible mass. The contour reported in the 2011 paper is shown in light blue. The 90% confidence limit from the 2014 paper is given in solid red, alongside the expected sensivity from the background model in light red. All other curves are due to data from other experiments; see the paper cited for more information.

CRESST2
Figure 2: WIMP parameter space for spin-independent WIMP-nucleon scattering, from 1407.3146v1.

Though this particular excess was ultimately not confirmed, these results overall present an optimistic picture for the dark matter search. Comparison between the limits from 2011 to 2014 show an much greater sensitivity for WIMP masses below 3 GeV, which were previously un-probed by other experiments. Additional detector improvements may result in even more stringent limit setting, shaping the dark matter search for future experiments.

 

Further Reading

 

Posted on

Black Holes enhance Dark Matter Annihilations

Title: Effect of Black Holes in Local Dwarf Spheroidal Galaxies on Gamma-Ray Constraints on Dark Matter Annihilation
Author: Alma X. Gonzalez-Morales, Stefano Profumo, Farinaldo S. Queiroz
Published: arXiv:1406.2424 [astro-ph.HE]
Upper bounds on dark matter annihilation from a combined analysis of 15 dwarf spheroidal galaxies for NFW (red) and Burkert (blue) DM density profiles.
Upper bounds on dark matter annihilation from a combined analysis of 15 dwarf spheroidal galaxies for NFW (red) and Burkert (blue) DM density profiles. Fig. 4 from arXiv:1406.2424.

In a previous ParticleBite we showed how dwarf spheroidal galaxies can tell us about dark matter interactions. As a short summary, these are dark matter-rich “satellite [sub-]galaxies” of the Milky Way that are ideal places to look for photons coming from dark matter annihilation into Standard Model particles. In this post we highlight a recent update to that analysis.

The rate at which a pair of dark matter particles annihilate in a galaxy is proportional to the square of the dark matter density. The authors point out that if the dwarf spheroidal galaxies contain intermediate mass black holes (\sim 10^4 times the mass of the sun), then its possible that the dark matter in the dwarf is more densely packed near the black hole. The authors redo the FERMI analysis for DM annihilation in dwarf spheroidals with 4 years of data (see our previous ParticleBite) with the assumption that these dwarfs contain a black hole consistent with their observed properties.

While the dwarf galaxies have little stellar content, one can use the visible stars to measure the stellar velocity dispersion, \sigma_*. As a benchmark, the authors use the Tremaine relation to determine the black hole mass as a function of the observed velocity dispersion,

Screen Shot 2014-06-11 at 6.51.24 PM

Here M_{\odot} is the mass of the sun. Given this mass and its effect on the dark matter density, they can then calculate the J factor that encodes the `astrophysical’ line of slight integral of the squared dark matter density to observers on the Earth. Following the FERMI analysis, authors then set bounds on the dark matter annihilation cross section as a function of the dark matter mass for 15 dwarf spheroidals:

DM annihilation cross-section constraints for the b ̄b final state, for individual dSph, and for a combined analysis of 15 galaxies, assuming an initial NFW DM density distributio
DM annihilation cross-section constraints for annihilation into a pair of b quarks, from 1406.2424 Fig. 1. The shaded band is the target cross section to obtain the correct dark matter relic density through thermal freeze out, the red box is the target cross section for a dark matter interpretation of an excess in gamma rays in the galactic center.

Observe that the bounds are significantly stronger than those in the original FERMI analysis. In particular, the strongest bounds thoroughly rule out the “40 GeV DM annihilating into a pair of b quarks” interpretation of a reported excess in gamma rays coming from the galactic center. These bounds, however, come with several caveats that are described in the paper. The largest caveat is that the existence of a black hole in any of these systems is only assumed. The authors note that numerical simulations suggest that there should be black holes in these systems, but to date there has been no verification of their existence.

Further Reading

  • We refer to the previous ParticleBite for introductory material on indirect detection of dark matter.
  • See this blog post at io9 for a public-level exposition and video of observational evidence for the supermassive black hole (much heavier than the intermediate mass black holes posited in the dwarf spheroidals) at the center of the Milky Way.
  • See Ullio et al. (astro-ph/0101481) for an early paper describing the effect of black holes on the dark matter distribution.
Posted on

Dark Matter Shining from the Dwarfs

Title: Dark Matter Constraints from Observations of 25 Milky Way Satellite Galaxies with the Fermi Large Area Telescope
Author: FERMI-LAT Collaboration
Published: Phys.Rev. D89 (2014) 042001 [arXiv:1310.0828]

Dark matter (DM) is `dark’ because it does not directly interact with light.  We suspect, however, that dark matter does interact with other Standard Model (SM) particles such as quarks and leptons. Since these SM particles do typically interact with photons, dark matter is indirectly luminous. More specifically, when two dark matter particles find each other and annihilate, their products include a spectrum photons that can be detected by telescopes. For typical `weakly-interacting massive particle’ DM candidates, these photons are in the GeV (γ-ray) range.

If dark matter interacts with the Standard Model, e.g. quarks, then its annihilation products include a spectrum of photons.
If dark matter interacts with the Standard Model, e.g. quarks, then its annihilation products include a spectrum of photons. Here we schematically show DM annihilating into quarks which shower into other colored `partons’ (quarks and gluons) that, in turn, become color-neutral hadrons. These then decay into light hadrons; the lightest of which (the neutral pion π) decays into two photons. Image adapted from D. Zeppenfeld (PiTP 05 lectures).

This type of indirect detection is a powerful handle to search for dark matter in the galaxy. The most promising place to search for these annihilation products are places where we expect a high density of dark matter, such as the galactic center. In fact, there have been recent hints for precisely this signal (see, e.g. this astrobite). Unfortunately, the galactic center is a very complicated environment with lots of other sources of GeV-scale photons that can make a DM interpretation tricky without additional checks.

Fortunately, there are other galactic objects that are dense with dark matter and have relatively little stellar (visible) matter: dwarf spheroidals. These satellite galaxies of the Milky Way are ideal laboratories for dark matter annihilation. While they have less dark matter density than the galactic center, they also have far fewer background photons from ordinary matter. Our tool of choice is the space-based Fermi-Large Area Telescope which is sensitive to photons between 0.03 — 300 GeV and surveys the entire sky every three hours.

Fig 1 of arXiv:1310.0828
Map of known dwarf spheroidals over a ‘heat map’ of Fermi gamma-ray data. Image from 1310.0828.

The photon flux from dark matter annihilation is a product of three factors:

Photon flux
Photon flux from DM annihilation.

The “particle physics factor” describes the dark matter properties: its mass and annihilation rate. The dN_\gamma/dE_\gamma factor describes the spectrum of photons coming from the DM annihilation products. The “astrophysics” factor is a line of sight integral along the dark matter density \rho. Note that the \rho^2 from this factor and the  m_\chi^{-2} in the particle physics factor is simply the dark matter number density; the photon flux depends on how likely it is for DM particles to find each other. The astrophysics factor is sometimes called a J factor. For some of the dwarfs astronomers can determine the J factor based on the kinematics of the [few] stellar objects in the dwarf spheroidal.

One may use the morphology—or spatial distribution of dark matter—to help subtract background photons and fit data. For this ParticleBite we won’t discuss this step further except to emphasize that these fits are where all the astrophysics “muscle” enters. Each dwarf individually sets bounds on the dark matter profile, but one can combine (or “stack”) these results into a combined bound for each DM annihilation final state. The bounds differ depending on these annihilation products because each type of particle produces a different spectrum of photons that must be re-fit relative to the background. The dark matter mass controls the energy with which the ‘primary’ annihilation products are produced so that heavier dark matter masses yield more energetic photons.

blahblah
Combined dwarf spheroidal bounds on the annihilation cross section (roughly the rate of DM annihilation) as a function of the dark matter mass for a choice of DM annihilation products. Image from 1310.0828.

In the above plots, the green and yellow bands represent the approximate expected 1σ and 2σ sensitivity while the solid black line is the observed bound. There is a slight excess at lower masses, though the most optimistic excess in the b-quark channel has a significance of TS ~ 8.7, where TS is a ‘test statistic’ measure introduced in the paper. The relevant comparison is that TS ~ 25 is the standard Fermi uses for a discovery, so this excess should be understood to be fairly modest. (Note that the paper also notes that the statistical analysis underestimates statistical significance so that if one were to convert this into p-values or σ, one would overestimate the significance.)

Note further that the “stacked” analysis is most sensitive to those dwarfs with the largest J factors. Of these, half showed an excess while the other half were consistent with no excess.

The most important feature of the above plots is the horizontal dashed line. This line represents the dark matter annihilation cross section (“annihilation rate”) that one predicts based on the requirement that the observed dark matter density is set by this annihilation process. (There are ways around this, but it remains the simplest and most natural possibility.) The relevant bounds on the dark matter models, then, comes from looking at the point where the solid line and the dashed horizontal line meet. Dark matter masses to the left (i.e. less than) this value are disfavored in the simplest models.

For example, for dark matter that annihilates to b-quarks, one finds that the dwarf spheroidals set a lower limit on the dark matter mass of around 10 Gev. We note that this bound based on 4 years of Fermi data is weaker than the previously published 2 year results due, in part, to a revised analysis.

The future? A gamma ray excess in the galactic center (see, e.g. this astrobite) may possibly be interpreted as a signal of dark matter with mass of around 40 GeV annihilating into b quarks. At the moment the dwarf spheroidal bounds are to weak to probe this region. Will it ever? Since Fermi samples the entire sky, any newly identified dwarf spheroidal (e.g. from the Sloan Digital Sky Survey) automatically makes the full 4 year dataset for that dwarf available. Since the bounds scale like \sqrt{N} (in the DM mass range below 200 GeV), one may roughly estimate the future sensitivity to the 40 GeV mass range as requiring 16 times more data. If we consider the next 4 years (doubling the observation time), this would require roughly 4 times more dwarfs to be identified. (See, e.g. this talk for a discussion.)

Further reading: some useful references for indirect detection of dark matter