Dark Matter Shining from the Dwarfs

Dark matter (DM) is `dark’ because it does not directly interact with light.  We suspect, however, that dark matter does interact with other Standard Model (SM) particles such as quarks and leptons. Since these SM particles do typically interact with photons, dark matter is indirectly luminous. More specifically, when two dark matter particles find each other and annihilate, their products include a spectrum photons that can be detected by telescopes. For typical `weakly-interacting massive particle’ DM candidates, these photons are in the GeV (γ-ray) range.

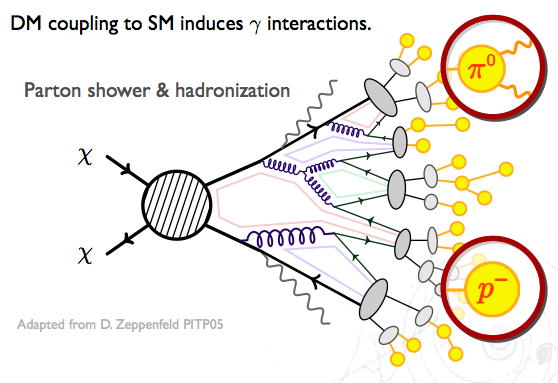
This type of indirect detection is a powerful handle to search for dark matter in the galaxy. The most promising place to search for these annihilation products are places where we expect a high density of dark matter, such as the galactic center. In fact, there have been recent hints for precisely this signal (see, e.g. this astrobite). Unfortunately, the galactic center is a very complicated environment with lots of other sources of GeV-scale photons that can make a DM interpretation tricky without additional checks.

Fortunately, there are other galactic objects that are dense with dark matter and have relatively little stellar (visible) matter: dwarf spheroidals. These satellite galaxies of the Milky Way are ideal laboratories for dark matter annihilation. While they have less dark matter density than the galactic center, they also have far fewer background photons from ordinary matter. Our tool of choice is the space-based Fermi-Large Area Telescope which is sensitive to photons between 0.03 — 300 GeV and surveys the entire sky every three hours.

The photon flux from dark matter annihilation is a product of three factors:

The “particle physics factor” describes the dark matter properties: its mass and annihilation rate. The factor describes the spectrum of photons coming from the DM annihilation products. The “astrophysics” factor is a line of sight integral along the dark matter density . Note that the  from this factor and the   in the particle physics factor is simply the dark matter number density; the photon flux depends on how likely it is for DM particles to find each other. The astrophysics factor is sometimes called a J factor. For some of the dwarfs astronomers can determine the J factor based on the kinematics of the [few] stellar objects in the dwarf spheroidal.

One may use the morphology—or spatial distribution of dark matter—to help subtract background photons and fit data. For this ParticleBite we won’t discuss this step further except to emphasize that these fits are where all the astrophysics “muscle” enters. Each dwarf individually sets bounds on the dark matter profile, but one can combine (or “stack”) these results into a combined bound for each DM annihilation final state. The bounds differ depending on these annihilation products because each type of particle produces a different spectrum of photons that must be re-fit relative to the background. The dark matter mass controls the energy with which the ‘primary’ annihilation products are produced so that heavier dark matter masses yield more energetic photons.

In the above plots, the green and yellow bands represent the approximate expected 1σ and 2σ sensitivity while the solid black line is the observed bound. There is a slight excess at lower masses, though the most optimistic excess in the b-quark channel has a significance of TS ~ 8.7, where TS is a ‘test statistic’ measure introduced in the paper. The relevant comparison is that TS ~ 25 is the standard Fermi uses for a discovery, so this excess should be understood to be fairly modest. (Note that the paper also notes that the statistical analysis underestimates statistical significance so that if one were to convert this into p-values or σ, one would overestimate the significance.)

Note further that the “stacked” analysis is most sensitive to those dwarfs with the largest J factors. Of these, half showed an excess while the other half were consistent with no excess.

The most important feature of the above plots is the horizontal dashed line. This line represents the dark matter annihilation cross section (“annihilation rate”) that one predicts based on the requirement that the observed dark matter density is set by this annihilation process. (There are ways around this, but it remains the simplest and most natural possibility.) The relevant bounds on the dark matter models, then, comes from looking at the point where the solid line and the dashed horizontal line meet. Dark matter masses to the left (i.e. less than) this value are disfavored in the simplest models.

For example, for dark matter that annihilates to b-quarks, one finds that the dwarf spheroidals set a lower limit on the dark matter mass of around 10 Gev. We note that this bound based on 4 years of Fermi data is weaker than the previously published 2 year results due, in part, to a revised analysis.

The future? A gamma ray excess in the galactic center (see, e.g. this astrobite) may possibly be interpreted as a signal of dark matter with mass of around 40 GeV annihilating into b quarks. At the moment the dwarf spheroidal bounds are to weak to probe this region. Will it ever? Since Fermi samples the entire sky, any newly identified dwarf spheroidal (e.g. from the Sloan Digital Sky Survey) automatically makes the full 4 year dataset for that dwarf available. Since the bounds scale like (in the DM mass range below 200 GeV), one may roughly estimate the future sensitivity to the 40 GeV mass range as requiring 16 times more data. If we consider the next 4 years (doubling the observation time), this would require roughly 4 times more dwarfs to be identified. (See, e.g. this talk for a discussion.)

Further reading: some useful references for indirect detection of dark matter

• TASI 2012 Lectures on Astrophysical Probes of Dark Matter
• Saas-Fee Lecture Notes: Multi-messenger Astronomy and Dark Matter
• Cosmic Frontier Indirect Dark Matter Detection Working Group Summary

Print Friendly