Posted on

The P5 Report & The Future of Particle Physics (Part 1)

Particle physics is the epitome of ‘big science’. To answer our most fundamental questions out about physics requires world class experiments that push the limits of whats technologically possible. Such incredible sophisticated experiments, like those at the LHC, require big facilities to make them possible,  big collaborations to run them, big project planning to make dreams of new facilities a reality, and committees with big acronyms to decide what to build.

Enter the Particle Physics Project Prioritization Panel (aka P5) which is tasked with assessing the landscape of future projects and laying out a roadmap for the future of the field in the US. And because these large projects are inevitably an international endeavor, the report they released last week has a large impact on the global direction of the field. The report lays out a vision for the next decade of neutrino physics, cosmology, dark matter searches and future colliders. 

P5 follows the community-wide brainstorming effort known as the Snowmass Process in which researchers from all areas of particle physics laid out a vision for the future. The Snowmass process led to a particle physics ‘wish list’, consisting of all the projects and research particle physicists would be excited to work on. The P5 process is the hard part, when this incredibly exciting and diverse research program has to be made to fit within realistic budget scenarios. Advocates for different projects and research areas had to make a case of what science their project could achieve and a detailed estimate of the costs. The panel then takes in all this input and makes a set of recommendations of how the budget should be allocated, what should projects be realized and what hopes are dashed. Though the panel only produces a set of recommendations, they are used quite extensively by the Department of Energy which actually allocates funding. If your favorite project is not endorsed by the report, its very unlikely to be funded. 

An computer generate graphic showing two sprays of particles being injected from a single center point
The P5 report also created an awesome graphic that contains symbolism for the different aspects of the plan. The left  side depicts oscillating neutrinos and the shape of the Higgs potential. The right side depicts dark matter and the large scale structure of the universe. The central ball of light is supposed to represent discoveries of the unknown. Source

Particle physics is an incredibly diverse field, covering sub-atomic to cosmic scales, so recommendations are divided up into several different areas. In this post I’ll cover the panel’s recommendations for neutrino physics and the cosmic frontier. Future colliders, perhaps the spiciest topic, will be covered in a follow up post.

The Future of Neutrino Physics

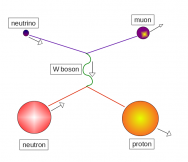
For those in the neutrino physics community all eyes were on the panels recommendations regarding the Deep Underground Neutrino Experiment (DUNE). DUNE is the US’s flagship particle physics experiment for the coming decade and aims to be the definitive worldwide neutrino experiment in the years to come. A high powered beam of neutrinos will be produced at Fermilab and sent 800 miles through the earth’s crust towards several large detectors placed in a mine in South Dakota. Its a much bigger project than previous neutrino experiments, unifying essentially the entire US community into a single collaboration.

DUNE is setup to produce world leading measurements of neutrino oscillations, the property by which neutrinos produced in one ‘flavor state’, (eg an electron-neutrino) gradually changes its state with sinusoidal probability (eg into a muon neutrino) as it propagates through space. This oscillation is made possible by a simple quantum mechanical weirdness: neutrino’s flavor state, whether it couples to electrons muons or taus, is not the same as its mass state. Neutrinos of a definite mass are therefore a mixture of the different flavors and visa versa.

Detailed measurements of this oscillation are the best way we know to determine several key neutrino properties. DUNE aims to finally pin down two crucial neutrino properties: their ‘mass ordering’, which will solidify how the different neutrino flavors and measured mass differences all fit together, and their ‘CP-violation’ which specifies whether neutrinos and their anti-matter counterparts behave the same or not. DUNE’s main competitor is the Hyper-Kamiokande experiment in Japan, another next-generation neutrino experiment with similar goals.

A depiction of the DUNE experiment. A high intensity proton beam at Fermilab is used to create a concentrated beam of neutrinos which are then sent through 800 miles of the Earth’s crust towards detectors placed deep underground South Dakota. Source

Construction of the DUNE experiment has been ongoing for several years and unfortunately has not been going quite as well as hoped. It has faced significant schedule delays and cost overruns. DUNE is now not expected to start taking data until 2031, significantly behind Hyper-Kamiokande’s projected 2027 start. These delays may lead to Hyper-K making these definitive neutrino measurements years before DUNE, which would be a significant blow to the experiment’s impact. This left many DUNE collaborators worried about its broad support from the community.

It came as a relief then when P5 report re-affirmed the strong science case for DUNE, calling it the “ultimate long baseline” neutrino experiment. The report strongly endorsed the completion of the first phase of DUNE. However, it recommended a pared-down version of its upgrade, advocating for an earlier beam upgrade in lieu of additional detectors. This re-imagined upgrade will still achieve the core physics goals of the original proposal with a significant cost savings. With this report, and news that the beleaguered underground cavern construction in South Dakota is now 90% complete, was certainly welcome holiday news to the neutrino community. This is also sets up a decade-long race between DUNE and Hyper-K to be the first to measure these key neutrino properties.

Cosmic Implications

While we normally think of particle physics as focused on the behavior of sub-atomic particles, its really about the study of fundamental forces and laws, no matter the method. This means that telescopes to study the oldest light in the universe, the Cosmic Microwave Background (CMB), fall into the same budget category as giant accelerators studying sub-atomic particles. Though the experiments in these two areas look very different, the questions they seek to answer are cross-cutting. Understanding how particles interact at very high energies helps us understand the earliest moments of the universe, when such particles were all interacting in a hot dense plasma. Likewise, by studying the these early moments of the universe and its large-scale evolution can tell us about what kinds of particles and forces are influencing its dynamics. When asking fundamental questions about the universe, one needs both the sharpest microscopes and the grandest panoramas possible.

The most prominent example of this blending of the smallest and largest scales in particle physics is dark matter. Some of our best evidence for dark matter comes analyzing the cosmic microwave background to determine how the primordial plasma behaved. These studies showed that some type of ‘cold’, matter that doesn’t interact with light, aka dark matter, was necessary to form the first clumps that eventually seeded the formation of galaxies. Without it, the universe would be much more soup-y and structureless than what we see to today.

The “cosmic web” galaxy clusters from the Millenium simulation. Measuring and understanding this web can tell us a lot about the fundamental constituents of the universe. Source

To determine what dark matter is then requires an attack from two fronts: design experiments here on earth attempting directly detect it, and further study its cosmic implications to look for more clues as to its properties.

The panel recommended next generation telescopes to study the CMB as a top priority. The so called ‘Stage 4’ CMB experiment would deploy telescopes in both the south pole and Chile’s Atacama desert to better characterize sources of atmospheric noise. The CMB has been studied extensively before, but the increased precision of CMS-S4 could shed light on mysteries like dark energy, dark matter, inflation, and the recent Hubble Tension. Given the past fruitfulness of these efforts, I think few doubted the science case for such a next generation experiment.

A mockup of one of the CMS-S4 telescopes which will be based in the Chilean desert. Note the person for scale on the right (source)

The P5 report recommended a suite of new dark matter experiments in the next decade, including the ‘ultimate’ liquid Xenon based dark matter search. Such an experiment would follow in the footsteps of massive noble gas experiments like LZ and XENONnT which have been hunting for a favored type of dark matter called WIMP’s for the last few decades. These experiments essentially build giant vats of liquid Xenon, carefully shield from any sources of external radiation, and look for signs of dark matter particles bumping into any of the Xenon atoms. The larger the vat of Xenon, the higher chance a dark matter particle will bump into something. Current generation experiments have ~7 tons of Xenon, and the next generation experiment would be even larger. The next generation aims to reach the so called ‘neutrino floor’, the point as which the experiments would be sensitive enough to observe astrophysical neutrinos bumping into the Xenon. Such neutrino interactions would look extremely similar to those of dark matter, and thus represent an unavoidable background which would signal the ultimate sensitivity of this type of experiment. WIMP’s could still be hiding in a basement below this neutrino floor, but finding them would be exceedingly difficult.

A photo of the current XENONnT experiment. This pristine cavity is then filled with liquid Xenon and closely monitored for signs of dark matter particles bumping into one of the Xenon atoms. Credit: XENON Collaboration

WIMP’s are not the only dark matter candidates in town, and recent years have also seen an explosion of interest in the broad range of dark matter possibilities, with axions being a prominent example. Other kinds of dark matter could have very different properties than WIMPs and have had much fewer dedicated experiments to search for them. There is ‘low hanging fruit’ to pluck in the way of relatively cheap experiments which can achieve world-leading sensitivity. Previously, these ‘table top’ sized experiments had a notoriously difficult time obtaining funding, as they were often crowded out of the budgets by the massive flagship projects. However, small experiments can be crucial to ensuring our best chance of dark matter discovery, as they fill in the blinds pots missed by the big projects.

The panel therefore recommended creating a new pool of funding set aside for these smaller scale projects. Allowing these smaller scale projects to flourish is important for the vibrancy and scientific diversity of the field, as the centralization of ‘big science’ projects can sometimes lead to unhealthy side effects. This specific recommendation also mirrors a broader trend of the report: to attempt to rebalance the budget portfolio to be spread more evenly and less dominated by the large projects.

A pie chart comparing the budget porfolio in 2023 (left) versus the projected budget in 2033 (right). Currently most of the budget is being taken up by the accelerator upgrades and cavern construction of DUNE, with some amount for the LHC upgrades. But by 2033 the panel recommends a much more equitable balance between different research area.

What Didn’t Make It

Any report like this comes with some tough choices. Budget realities mean not all projects can be funded. Besides the pairing down of some of DUNE’s upgrades, one of the biggest areas that was recommended against were ‘accessory experiments at the LHC’. In particular, MATHUSULA and the Forward Physics Facility were two experiments that proposed to build additional detectors near already existing LHC collision points to look for particles that may be missed by the current experiments. By building new detectors hundreds of meters away from the collision point, shielded by concrete and the earth, they can obtained unique sensitivity to ‘long lived’ particles capable of traversing such distances. These experiments would follow in the footsteps of the current FASER experiment, which is already producing impressive results.

While FASER found success as a relatively ‘cheap’ experiment, reusing detector components from and situating itself in a beam tunnel, these new proposals were asking for quite a bit more. The scale of these detectors would have required new caverns to be built, significantly increasing the cost. Given the cost and specialized purpose of these detectors, the panel recommended against their construction. These collaborations may now try to find ways to pare down their proposal so they can apply to the new small project portfolio.

Another major decision by the panel was to recommend against hosting a new Higgs factor collider in the US. But that will discussed more in a future post.

Conclusions

The P5 panel was faced with a difficult task, the total cost of all projects they were presented with was three times the budget. But they were able to craft a plan that continues the work of the previous decade, addresses current shortcomings and lays out an inspiring vision for the future. So far the community seems to be strongly rallying behind it. At time of writing, over 2700 community members from undergraduates to senior researchers have signed a petition endorsing the panels recommendations. This strong show of support will be key for turning these recommendations into actual funding, and hopefully lobbying congress to even increase funding so that more of this vision can be realized.

For those interested the full report as well as executive summaries of different areas can be found on the P5 website. Members of the US particle physics community are also encouraged to sign the petition endorsing the recommendations here.

And stayed tuned for part 2 of our coverage which will discuss the implications of the report on future colliders!

Posted on

The Mini and Micro Boone Mystery, Part 1 Experiment

Title: “Search for an Excess of Electron Neutrino Interactions in MicroBooNE Using Multiple Final State Topologies”

Authors: The MiniBoone Collaboration

Reference: https://arxiv.org/abs/2110.14054

This is the first post in a series on the latest MicroBooNE results, covering the experimental side. Click here to read about the theory side. 

The new results from the MicroBoone experiment received a lot of excitement last week, being covered by several major news outlets. But unlike most physics news stories that make the press, it was a null result; they did not see any evidence for new particles or interactions. So why is it so interesting? Particle physics experiments produce null results every week, but what made this one newsworthy is that MicroBoone was trying to check the results from two previous experiments LSND and MiniBoone, that did see something anomalous with very high statistical evidence. If the LSND/MiniBoone result was confirmed, it would have been a huge breakthrough in particle physics, but now that it wasn’t many physicists are scratching their heads trying to make sense of these seemingly conflicting results. However, the MicroBoone experiment is not exactly the same as MiniBoone/LSND, and understanding the differences between the two sets of experiments may play an important role in unraveling this mystery.

Accelerator Neutrino Basics

All of these experiments are ‘accelerator neutrino experiments’, so lets first review what that means. Neutrino’s are ‘ghostly’ particles that are difficult to study (check out this post for more background on neutrinos).  Because they only couple through the weak force, neutrinos don’t like to interact with anything very much. So in order to detect them you need both a big detector with a lot of active material and a source with a lot of neutrinos. These experiments are designed to detect neutrinos produced in a human-made beam. To make the beam, a high energy beam of protons is directed at a target. These collisions produce a lot of particles, including unstable bound states of quarks like pions and kaons. These unstable particles have charge, so we can use magnets to focus them into a well-behaved beam.  When the pions and kaons decay they usually produce a muon and a muon neutrino. The beam of pions and kaons is pointed at an underground detector located a few hundred meters (or kilometers!) away, and then given time to decay. After they decay there will be a nice beam of muons and muon neutrinos. The muons can be stopped by some kind of shielding (like the earth’s crust), but the neutrinos will sail right through to the detector.

A diagram showing the basics of how a neutrino beam is made. Source

Nearly all of the neutrinos from the beam will still pass right through your detector, but a few of them will interact, allowing you to learn about their properties.

All of these experiments are considered ‘short-baseline’ because the distance between the neutrino source and the detector is only a few hundred meters (unlike the hundreds of kilometers in other such experiments). These experiments were designed to look for oscillation of the beam’s muon neutrinos into electron neutrinos which then interact with their detector (check out this post for some background on neutrino oscillations). Given the types of neutrinos we know about and their properties, this should be too short of a distance for neutrinos to oscillate, so any observed oscillation would be an indication something new (beyond the Standard Model) was going on.

The LSND + MiniBoone Anomaly

So the LSND and MiniBoone ‘anomaly’ was an excess of events above backgrounds that looked like electron neutrinos interacting with their detector. Both detectors were based on similar technology and were a similar distance from their neutrino source. Their detectors were essentially big tanks of mineral oil lined with light-detecting sensors.

An engineer styling inside the LSND detector. Source

At these energies the most common way neutrinos interact is to scatter against a neutron to produce a proton and a charged lepton (called a ‘charged current’ interaction). Electron neutrinos will produce outgoing electrons and muon neutrinos will produce outgoing muons.

A diagram of a ‘charged current’ interaction. A muon neutrino comes in and scatters against a neutron, producing a muon and a proton. Source

When traveling through the mineral oil these charged leptons will produce a ring of Cherenkov light which is detected by the sensors on the edge of the detector. Muons and electrons can be differentiated based on the characteristics of the Cherenkov light they emit. Electrons will undergo multiple scatterings off of the detector material while muons will not. This makes the Cherenkov rings of electrons ‘fuzzier’ than those of muons. High energy photons can produce electrons positron pairs which look very similar to a regular electron signal and are thus a source of background. 

A comparison of muon and electron Cherenkov rings from the Super-Kamiokande experiment. Electrons produce fuzzier rings than muons. Source

Even with a good beam and a big detector, the feebleness of neutrino interactions means that it takes a while to get a decent number of potential events. The MiniBoone experiment ran for 17 years looking for electron neutrinos scattering in their detector. In MiniBoone’s most recent analysis, they saw around 600 more events than would be expected if there were no anomalous electron neutrinos reaching their detector. The statistical significance of this excess, 4.8-sigma, was very high. Combining with LSND which saw a similar excess, the significance was above 6-sigma. This means its very unlikely this is a statistical fluctuation. So either there is some new physics going on or one of their backgrounds has been seriously under-estimated. This excess of events is what has been dubbed the ‘MiniBoone anomaly’.

The number of events seen in the MiniBoone experiment as a function of the energy seen in the interaction. The predicted number of events from various known background sources are shown in the colored histograms. The best fit to the data including the signal of anomalous oscillations is shown by the dashed line. One can see that at low energies the black data points lie significantly above these backgrounds and strongly favor the oscillation hypothesis.

The MicroBoone Result

The MicroBoone experiment was commissioned to verify the MiniBoone anomaly as well as test out a new type of neutrino detector technology. The MicroBoone is the first major neutrino experiment to use a ‘Liquid Argon Time Projection Chamber’ detector. This new detector technology allows more detailed reconstruction of what is happening when a neutrino scatters in the detector. The the active volume of the detector is liquid Argon, which allows both light and charge to propagate through it. When a neutrino scatters in the liquid Argon, scintillation light is produced that is collected in sensors. As charged particles created in the collision pass through the liquid Argon they ionize atoms they pass by. An electric field applied to the detector causes this produced charge to drift towards a mesh of wires where it can be collected. By measuring the difference in arrival time between the light and the charge, as well as the amount of charge collected at different positions and times, the precise location and trajectory of the particles produced in the collision can be determined. 

A beautiful reconstructed event in the MicroBoone detector. The colored lines show the tracks of different particles produced in the collision, all coming from a single point where the neutrino interaction took place. One can also see that one of the tracks produced a shower of particles away from the interaction vertex.

This means that unlike the MiniBoone and LSND, MicroBoone can see not just the lepton, but also the hadronic particles (protons, pions, etc) produced when a neutrino scatters in their detector. This means that the same type of neutrino interaction actually looks very different in their detector. So when they went to test the MiniBoone anomaly they adopted multiple different strategies of what exactly to look for. In the first case they looked for the type of interaction that an electron neutrino would have most likely produced: an outgoing electron and proton whose kinematics match those of a charged current interaction. Their second set of analyses, designed to mimic the MiniBoone selection, are slightly more general. They require one electron and any number of protons, but no pions. Their third analysis is the most general and requires an electron along with anything else. 

These different analyses have different levels of sensitivity to the MiniBoone anomaly, but all of them are found to be consistent with a background-only hypothesis: there is no sign of any excess events. Three out of four of them even see slightly less events than the expected background. 

A summary of the different MicroBoone analyses. The Y-axis shows the ratio of observed to expected number of events expected if there was only background present. The red lines show the excess predicted to be seen if the MiniBoone anomaly produced a signal in each channel. One can see that the black data points are much more consistent with the grey bands showing the background only prediction than amount predicted if the MiniBoone anomaly was present.

Overall the MicroBoone data rejects the hypothesis that the MiniBoone anomaly is due to electron neutrino charged current interactions at quite high significance (>3sigma). So if its not electron neutrinos causing the MiniBoone anomaly, what is it?

What’s Going On?

Given that MicroBoone did not see any signal, many would guess that MiniBoone’s claim of an excess must be flawed and they have underestimated one of their backgrounds. Unfortunately it is not very clear what that could be. If you look at the low-energy region where MiniBoone has an excess, there are three major background sources: decays of the Delta baryon that produce a photon (shown in tan), neutral pions decaying to pairs of photons (shown in red), and backgrounds from true electron neutrinos (shown in various shades of green). However all of these sources of background seem quite unlikely to be the source of the MiniBoone anomaly.

Before releasing these results, MicroBoone performed a dedicated search for Delta baryons decaying into photons, and saw a rate in agreement with the theoretical prediction MiniBoone used, and well below the amount needed to explain the MiniBoone excess.

Backgrounds from true electron neutrinos produced in the beam, as well as from the decays of muons, should not concentrate only at low energies like the excess does, and their rate has also been measured within MiniBoone data by looking at other signatures.

The decay of a neutral pions can produce two photons, and if one of them escapes detection, a single photon will mimic their signal. However one would expect that it would be more likely that photons would escape the detector near its edges, but the excess events are distributed uniformly in the detector volume.

So now the mystery of what could be causing this excess is even greater. If it is a background, it seems most likely it is from an unknown source not previously considered. As will be discussed in our part 2 post, its possible that MiniBoone anomaly was caused by a more exotic form of new physics; possibly the excess events in MiniBoone were not really coming from the scattering of electron neutrinos but something else that produced a similar signature in their detector. Some of these explanations included particles that decayed into pairs of electrons or photons. These sorts of explanations should be testable with MicroBoone data but will require dedicated analyses for their different signatures.

So on the experimental side, we now we are left to scratch our heads and wait for new results from MicroBoone that may help get to the bottom of this.

Click here for part 2 of our MicroBoone coverage that goes over the theory side of the story!

Read More

“Is the Great Neutrino Puzzle Pointing to Multiple Missing Particles?” – Quanta Magazine article on the new MicroBoone result

“Can MiniBoone be Right?” – Resonaances blog post summarizing the MiniBoone anomaly prior to the the MicroBoone results

A review of different types of neutrino detectors – from the T2K experiment

Posted on

How to find invisible particles in a collider

 You might have heard that one of the big things we are looking for in collider experiments are ever elusive dark matter particles. But given that dark matter particles are expected to interact very rarely with regular matter, how would you know if you happened to make some in a collision? The so called ‘direct detection’ experiments have to operate giant multi-ton detectors in extremely low-background environments in order to be sensitive to an occasional dark matter interaction. In the noisy environment of a particle collider like the LHC, in which collisions producing sprays of particles happen every 25 nanoseconds, the extremely rare interaction of the dark matter with our detector is likely to be missed. But instead of finding dark matter by seeing it in our detector, we can instead find it by not seeing it. That may sound paradoxical, but its how most collider based searches for dark matter work. 

The trick is based on every physicists favorite principle: the conservation of energy and momentum. We know that energy and momentum will be conserved in a collision, so if we know the initial momentum of the incoming particles, and measure everything that comes out, then any invisible particles produced will show up as an imbalance between the two. In a proton-proton collider like the LHC we don’t know the initial momentum of the particles along the beam axis, but we do that they were traveling along that axis. That means that the net momentum in the direction away from the beam axis (the ‘transverse’ direction) should be zero. So if we see a momentum imbalance going away from the beam axis, we know that there is some ‘invisible’ particle traveling in the opposite direction.

A sketch of what the signature of an invisible particle would like in a detector. Note this is a 2D cross section of the detector, with the beam axis traveling through the center of the diagram. There are two signals measured in the detector moving ‘up’ away from the beam pipe. Momentum conservation means there must have been some particle produced which is traveling ‘down’ and was not measured by the detector. Figure borrowed from here  

We normally refer to the amount of transverse momentum imbalance in an event as its ‘missing momentum’. Any collisions in which an invisible particle was produced will have missing momentum as tell-tale sign. But while it is a very interesting signature, missing momentum can actually be very difficult to measure. That’s because in order to tell if there is anything missing, you have to accurately measure the momentum of every particle in the collision. Our detectors aren’t perfect, any particles we miss, or mis-measure the momentum of, will show up as a ‘fake’ missing energy signature. 

A picture of a particularly noisy LHC collision, with a large number of tracks
Can you tell if there is any missing energy in this collision? Its not so easy… Figure borrowed from here

Even if you can measure the missing energy well, dark matter particles are not the only ones invisible to our detector. Neutrinos are notoriously difficult to detect and will not get picked up by our detectors, producing a ‘missing energy’ signature. This means that any search for new invisible particles, like dark matter, has to understand the background of neutrino production (often from the decay of a Z or W boson) very well. No one ever said finding the invisible would be easy!

However particle physicists have been studying these processes for a long time so we have gotten pretty good at measuring missing energy in our events and modeling the standard model backgrounds. Missing energy is a key tool that we use to search for dark matter, supersymmetry and other physics beyond the standard model.

Read More:

“What happens when energy goes missing?” ATLAS blog post by Julia Gonski

“How to look for supersymmetry at the LHC“, blog post by Matt Strassler

“Performance of missing transverse momentum reconstruction with the ATLAS detector using proton-proton collisions at √s = 13 TeV” Technical Paper by the ATLAS Collaboration

“Search for new physics in final states with an energetic jet or a hadronically decaying W or Z boson and transverse momentum imbalance at √s= 13 TeV” Search for dark matter by the CMS Collaboration

Posted on

Maleficent dark matter: Part I

We might not have gotten here without dark matter. It was the gravitational pull of dark matter, which makes up most of the mass of galactic structures, that kept heavy elements — the raw material of Earth-like rocky planets — from flying away after the first round of supernovae at the advent of the stelliferous era. Without this invisible pull, all structures would have been much smaller than seen today, and stars much more rare.

Thus with knowledge of dark matter comes existential gratitude. But the microscopic identity of dark matter is one of the biggest scientific enigmas of our times, and what we don’t know could yet kill us. This two-part series is about the dangerous end of our ignorance, reviewing some inconvenient prospects sketched out in the dark matter literature. Reader discretion is advised.

[Note: The scenarios outlined here are based on theoretical speculations of dark matter’s identity. Such as they are, these are unlikely to occur, and even if they do, extremely unlikely within the lifetime of our species, let alone that of an individual. In other words, nobody’s sleep or actuarial tables need be disturbed.]

The dark matter wind could blow in mischief. Image source: Freese et al.

Carcinogenic dark matter

Maurice Goldhaber quipped that “you could feel it in your bones” that protons are cosmologically long-lived, as otherwise our bodies would have self-administered a lethal dose of ionizing radiation. (This observation sets a lower limit on the proton lifetime at a comforting 10^7 times the age of the universe.) Could we laugh similarly about dark matter? The Earth is probably amid a wind of particle dark matter, a wind that could trigger fatal ionization in our cells if encountered too frequently. The good news is that if dark matter is made of weakly interacting massive particles (WIMPs), K. Freese and C. Savage report safety: “Though WIMP interactions are a source of radiation in the body, the annual exposure is negligible compared to that from other natural sources (including radon and cosmic rays), and the WIMP collisions are harmless to humans.“

The bad news is that the above statement assumes dark matter is distributed smoothly in the Galactic halo. There are interesting cosmologies in which dark matter collects in high-density “clumps” (a.k.a. “subhalos”, “mini-halos”,  or “mini-clusters”). According to J. I. Collar, the Earth encountering these clumps every 30–100 million years could explain why mass extinctions of life occur periodically on that timescale. During transits through the clumps, dark matter particles could undergo high rates of elastic collisions with nuclei in life forms, injecting 100–200 keV of energy per micrometer of transit, just right to “induce a non-negligible amount of radiation damage to all living tissue“. We are in no hurry for the next dark clump.

Eruptive dark matter

If your dark matter clump doesn’t wipe out life efficiently via cancer,  A. Abbas and S. Abbas recommend waiting another five million years. It takes that long for the clump dark matter to gravitationally capture in Earth, settle in its core, self-annihilate, and heat the mantle, setting off planet-wide volcanic fireworks. The resulting chain of events would end, as the authors rattle off enthusiastically, in “the depletion of the ozone layer, global temperature changes, acid rain, and a decrease in surface ocean alkalinity.”

Dark matter settling in the Earth’s core could spell doom. Image source: J. Bramante & A. Goodman.

Armageddon dark matter

If cancer and volcanoes are not dark matter’s preferred methods of prompting mass extinction, it could get the job done with old-fashioned meteorite impacts.

It is usually supposed that dark matter occupies a spherical halo that surrounds the visible, star-and-gas-crammed, disk of the Milky Way.  This baryonic pancake was formed when matter, starting out in a spinning sphere, cooled down by radiating photons and shrunk in size along the axis of rotation; due to conservation of angular momentum the radial extent was preserved. No such dissipative process is known to govern dark matter, thus it retains its spherical shape. However, a small component of dark matter might have still cooled by emitting some unseen radiation such as “dark photons“. That would result in a “dark disk” sub-structure co-existing in the Galactic midplane with the visible disk. Every 35 million years the Solar System crosses the Galactic midplane, and when that happens, a dark disk of surface density of 10 M_\odot/pc^2 could tidally perturb the Oort Cloud and send comets shooting toward the inner planets, causing periodic mass extinctions. So suggest L. Randall and M. Reece, whose arXiv comment “4 figures, no dinosaurs” is as much part of the particle physics lore as Randall’s book that followed the paper, Dark Matter and the Dinosaurs.

We note in passing that SNOLAB, the underground laboratory in Sudbury, ON that houses the dark matter experiments DAMIC, DEAP, and PICO, and future home of NEWS-G, SENSEI,  Super-CDMS and ARGO, is located in the Creighton Mine — where ore deposits were formed by a two billion year-old comet impact. Perhaps the dark disk nudges us to detect its parent halo.

A drift (horizontal passage) in Creighton Mine, 2.1 km underground. Around the corner is SNOLAB, where several experiments searching for dark matter are located. The mine owes its existence to a meteorite impact — perhaps triggered by a Galactic disk of dark matter. Photo: N. Raj.

——————
In the second part of the series we will look — if we’re still here — at more surprises that dark matter could have planned for us. Stay tuned.

Bibliography.

[1] Dark Matter collisions with the Human Body, K. Freese & D. Savage, Phys.Lett.B 717 (2012) 25-28.

[2] Clumpy cold dark matter and biological extinctions, J. I. Collar, Phys.Lett.B 368 (1996) 266-269.

[3] Volcanogenic dark matter and mass extinctions, S. Abbas & A. Abbas, Astropart.Phys. 8 (1998) 317-320

[4] Dark Matter as a Trigger for Periodic Comet Impacts, L. Randall & M. Reece, Phys.Rev.Lett. 112 (2014) 161301

[5] Dark Matter and the Dinosaurs, L. Randall, Harper Collins: Ecco Press‎ (2015)

Posted on

Adjectivous dark matter

How would you describe dark matter in one word? Mysterious? Ubiquitous? Massive? Theorists often try to settle the question in the title of a paper — with a single adjective. Thanks to this penchant we now have the possibility of cannibal dark matter. To be sure, in the dark world eating one’s own kind is not considered forbidden, not even repulsive. Just a touch selfish, maybe. And it could still make you puffy — if you’re inflatable and not particularly inelastic. Otherwise it makes you plain superheavy.

Below are more uni-verbal dark matter candidates in the literature. Some do make you wonder if the title preceded the premise. But they all remind you of how much fun it is, this quest for dark matter’s identity. Keep an eye out on arXiv for these gems!

anapole, asymmetric, atomic, brane-world, charged, co-interacting, coloured, cryptobaryonic, disformal, fluid, freeze-twin, gluequark, GUTzilla, homeopathic, impeded, inflaxion, Kaluza-Klein, luminous, macro, minimal, monodromy, \nu-inflaton, parafermionic, relaxion, resonant, self-destructing, self-interacting, singlet-doublet, spectator, super-cool, technicolor, topological, undulating, unparticle, wave.

This image has an empty alt attribute; its file name is cannibnoun.png
Dark matter, in addition to consuming physicists, could also be cannibal. Image: Gan Khoon Lay, Noun Project.

Posted on

Crystals are dark matter’s best friends

Article title: “Development of ultra-pure NaI(Tl) detector for COSINE-200 experiment”

Authors: B.J. Park et el.

Reference: arxiv:2004.06287

The landscape of direct detection of dark matter is a perplexing one; all experiments have so far come up with deafening silence, except for a single one which promises a symphony. This is the DAMA/LIBRA experiment in Gran Sasso, Italy, which has been seeing an annual modulation in its signal for two decades now.

Such an annual modulation is as dark-matter-like as it gets. First proposed by Katherine Freese in 1987, it would be the result of earth’s motion inside the galactic halo of dark matter in the same direction as the sun for half of the year and in the opposite direction during the other half. However, DAMA/LIBRA’s results are in conflict with other experiments – but with the catch that none of those used the same setup. The way to settle this is obviously to build more experiments with the DAMA/LIBRA setup. This is an ongoing effort which ultimately focuses on the crystals at its heart.

Cylindrical crystals wrapped in reflector, bounded by photomultipliers (PMTs) and surrounded by scintillators. (COSINE-100)

The specific crystals are made of the scintillating material thallium-doped sodium iodide, NaI(Tl). Dark matter particles, and particularly WIMPs, would collide elastically with atomic nuclei and the recoil would give off photons, which would eventually be captured by photomultiplier tubes at the ends of each crystal.

Right now a number of NaI(Tl)-based experiments are at various stages of preparation around the world, with COSINE-100 at the Yangyang mountain, S.Korea, already producing negative results. However, these are still not on equal footing with DAMA/LIBRA’s because of higher backgrounds at COSINE-100. What is the collaboration to do, then? The answer is focus even more on the crystals and how they are prepared.

Setup of the COSINE-100 experiment. (COSINE-100)

Over the last couple of years some serious R&D went into growing better crystals for COSINE-200, the planned upgrade of COSINE-100. Yes, a crystal is something that can and does grow. A seed placed inside the raw material, in this case NaI(Tl) powder, leads it to organize itself around the seed’s structure over the next hours or days.

In COSINE-100 the most annoying backgrounds came from within the crystals themselves because of the production process, because of natural radioactivity, and because of cosmogenically induced isotopes. Let’s see how each of these was tackled during the experiment’s mission towards a radiopure upgrade.

Improved techniques of growing and preparing the crystals reduced contamination from the materials of the grower device and from the ambient environment. At the same time different raw materials were tried out to put the inherent contamination under control.

Among a handful of naturally present radioactive isotopes particular care was given to 40K. 40K can decay characteristically to an X-ray of 3.2keV and a γ-ray of 1,460keV, a combination convenient for tagging it to a large extent. The tagging is done with the help of 2,000 liters of liquid scintillator surrounding the crystals. However, if the γ-ray escapes the crystal then the left-behind X-ray will mimic the expected signal from WIMPs… Eventually the dangerous 40K was brought down to levels comparable to those in DAMA/LIBRA through the investigation of various techniques and first materials.

But the main source of radioactive background in COSINE-100 was isotopes such as 3H or 22Na created inside the crystals by cosmic ray muons, after their production. Now, their abundance was reduced significantly by two simple moves: the crystals were grown locally at a very low altitude and installed underground within a few weeks (instead of being transported from a lab at 1,400 meters above sea in Colorado). Moreover, most of the remaining cosmogenic background is to decay away within a couple of years.

Components of the background, and temporal evolution of the cosmogenic radioactivity. (Source)

Where are these efforts standing? The energy range of interest for testing the DAMA/LIBRA signal is 1-6keV. This corresponds to a background target of 1 count/kg/day/keV. After the crystals R&D, the achieved contamination was less than about 0.34 counts. In short, everything is ready for COSINE-100 to upgrade to COSINE-200 and test the annual modulation without the previous ambiguities that stood in the way.

Learn more:

More on DAMA/LIBRA in ParticleBites.

Cross-checking the modulation.

The COSINE-100 experiment.

First COSINE-100 results.

Posted on

Listening for axions

If dark matter actually consists of a new kind of particle, then the most up-and-coming candidate is the axion. The axion is a consequence of the Peccei-Quinn mechanism, a plausible solution to the “strong CP problem,” or why the strong nuclear force conserves the CP-symmetry although there are no reasons for it to. It is a very light neutral boson, named by Frank Wilczek after a detergent brand (in a move that obviously dates its introduction in the ’70s).

Axion decay in a magnetic field: the result is a photon. (Source.)

Most experiments that try to directly detect dark matter have looked for WIMPs (weakly interacting massive particles). However, as those searches have not borne fruit, the focus started turning to axions, which make for good candidates given their properties and the fact that if they exist, then they exist in multitudes throughout the galaxies. Axions “speak” to the QCD part of the Standard Model, so they can appear in interaction vertices with hadronic loops. The end result is that axions passing through a magnetic field will convert to photons.

In practical terms, their detection boils down to having strong magnets, sensitive electronics and an electromagnetically very quiet place at one’s disposal. One can then sit back and wait for the hypothesized axions to pass through the detector as earth moves through the dark matter halo surrounding the Milky Way. Which is precisely why such experiments are known as “haloscopes.”

Now, the most veteran haloscope of all published significant new results. Alas, it is still empty-handed, but we can look at why its update is important and how it was reached.

ADMX (Axion Dark Matter eXperiment) of the University of Washington has been around for a quarter-century. By listening for signals from axions, it progressively gnaws away at the space of allowed values for their mass and coupling to photons, focusing on an area of interest:

ADMX_results_2020
Latest exclusion limits on the axion mass and coupling to photons.

Unlike higher values, this area is not excluded by astrophysical considerations (e.g. stars cooling off through axion emission) and other types of experiments (such as looking for axions from the sun). In addition, the bands above the lines denoted “KSVZ” and “DFSZ” are special. They correspond to the predictions of two models with favorable theoretical properties. So, ADMX is dedicated to scanning this parameter space. And the new analysis added one more year of data-taking, making a significant dent in this ballpark.

As mentioned, the presence of axions would be inferred from a stream of photons in the detector. The excluded mass range was scanned by “tuning” the experiment to different frequencies, while at each frequency step longer observation times probed smaller values for the axion-photon coupling.

Two things that this search needs is a lot of quiet and some good amplification, as the signal from a typical axion is expected to be as weak as the signal from a mobile phone left on the surface of Mars (around 10-23W). The setup is indeed stripped of noise by being placed in a dilution refrigerator, which keeps its temperature at a few tenths of a degree above absolute zero. This is practically the domain governed by quantum noise, so advantage can be taken of the finesse of quantum technology: for the first time ADMX used SQUIDs, superconducting quantum interference devices, for the amplification of the signal.

The heart of the experiment inside the refrigerator. The resonant frequency of the cavity is tuned to match the photons -hopefully- given off by axions. (Source.)




In the end, a good chunk of the parameter space which is favored by the theory might have been excluded, but the haloscope is ready to look at the rest of it. Just think of how, one day, a pulse inside a small device in a university lab might be a messenger of the mysteries unfolding across the cosmos.

References:

Publication by the ADMX collaboration. (arXiv)

Learn more:

  1. The theory behind axions.
  2. The hitchhiker’s guide to the dilution refrigerator.
  3. Intro to KSVZ and DFSZ axions (and more).
  4. Resonant cavities.
Posted on

Quark nuggets of wisdom

Article title: “Dark Quark Nuggets”

Authors: Yang Baia, Andrew J. Long, and Sida Lu

Reference: arXiv:1810.04360

Information, gold and chicken. What do they all have in common? They can all come in the form of nuggets. Naturally one would then be compelled to ask: “what about fundamental particles? Could they come in nugget form? Could that hold the key to dark matter?” Lucky for you this has become the topic of some ongoing research.

A ‘nugget’ in this context refers to large macroscopic ‘clumps’ of matter formed in the early universe that could possibly survive up until the present day to serve as a dark matter candidate. Much like nuggets of the edible variety, one must be careful to combine just the right ingredients in just the right way. In fact, there are generally three requirements to forming such an exotic state of matter:

  1. (At least) two different vacuum states separated by a potential ‘barrier’ where a phase transition occurs (known as a first-order phase transition).
  2. A charge which is conserved globally which can accumulate in a small part of space.
  3. An excess of matter over antimatter on the cosmological scale, or in other words, a large non-zero macroscopic number density of global charge.

Back in the 1980s, before much work was done in the field of lattice quantum chromodynamics (lQCD), Edward Witten put forward the idea that the Standard Model QCD sector could in fact accommodate such an exotic form of matter. Quite simply this would occur at the early phase of the universe when the quarks undergo color confinement to form hadrons. In particular Witten’s were realized as large macroscopic clumps of ‘quark matter’ with a very large concentration of baryon number, N_B > 10^{30}. However, with the advancement of lQCD techniques, the phase transition in which the quarks become confined looks more like a continuous ‘crossover’ (i.e. a second-order phase transition), making the idea in the Standard Model somewhat unfeasible.

Theorists, particularly those interested in dark matter, are not confined (for lack of a better term) to the strict details of the Standard Model and most often look to the formation of sometimes complicated ‘dark sectors’ invisible to us but readily able to provide the much needed dark matter candidate.

Dark QCD?

The problem of obtaining a first-order phase transition to form our quark nuggets need not be a problem if we consider a QCD-type theory that does not interact with the Standard Model particles. More specifically, we can consider a set of dark quarks, dark gluons with arbitrary characteristics like masses, couplings, numbers of flavors or numbers of colors (which of course are quite settled for the Standard Model QCD case). In fact, looking at the numbers of flavors and colors of dark QCD in Figure 1, we can see in the white unshaded region a number of models that can exist with a first-order phase transition, as required to form these dark quark nuggets.

Figure 1: The white unshaded region corresponds to dark QCD models which may permit a first-order phase transition and thus the existence of ‘dark quark nuggets’.

As with normal quarks, the distinction between the two phases actually refers to a process known as chiral symmetry breaking. When the temperature of the universe cools to this particular scale, color confinement of quarks occurs around the same time, such that no single-color quark can be observed on its own – only in colorless bound states.

Forming a nugget

As we have briefly mentioned so far, the dark nuggets are formed as the universe undergoes a ‘dark’ phase transition from a phase where the dark color is unconfined to a phase where it is confined. At some critical temperature, due to the nature of first-order phase transitions, bubbles of the new confined phase (full of dark hadrons) begin to nucleate out of the dark quark-gluon plasma. The growth of these bubbles are driven by a difference in pressure, characteristic of the fact that the unconfined and confined phase vacuums states are of different energy. With this emerging bubble wall, the almost massless particles from the dark plasma scatter from the wall containing heavy dark (anti)baryons and hence a large amount of dark baryon number accumulates in this phase. Eventually, as these bubbles merge and coalesce, we would expect local regions of remaining dark quark-gluon plasma, unconfined and stable from collapse due to the Fermi degeneracy pressure (see reference below for more on this). An illustration is shown in Figure 2. Calculations with varying energy scales of confinement estimate their masses are anywhere between 10^{-7} to 10^{23} grams with radii from 10^{-15} to 10^8 cm and so can truly be classed as macroscopic dark objects!

Figure 2: Dark Quark Nuggets are a phase of unconfined dark quark-gluon plasma kept stable by the balance between Fermi degeneracy pressure and vacuum pressure from the separation between the unconfined and confined phases.

How do we know they could be there? 

There are a number of ways to infer the existence of dark quark nuggets, but two of the main ones are: (i) as a dark matter candidate and (ii) through probes of the dark QCD model that provides them. Cosmologically, the latter can imply the existence of a dark form of radiation which ultimately can lead to effects on the Cosmic Microwave Background Radiation (CMB). In a similar vein, one recent avenue of study today is the production of a steady background of gravitational waves emerging from the existence of a first-order phase transition – one of the key requirements for dark quark nugget formation. More importantly, they can be probed through astrophysical means if they share some coupling (albeit small) with the Standard Model particles. The standard technique of direct detection with Earth-based experiments could be the way to go – but furthermore, there may be the possibility of cosmic ray production from collisions of multiple dark quark nuggets. Among these are a number of other observations over the massive range of nugget sizes and masses shown in Figure 3.

Figure 3: Range of dark quark nugget masses and sizes and their possible detection methods.

To conclude, note that in such a generic framework, a number of well-motivated theories may predict (or in fact have unavoidable) instances of quark nuggets that may serve as interesting dark matter candidates with a lot of fun phenomenology to play with. It is only up to the theorist’s imagination where to go from here!

References and further reading:

Posted on

The lighter side of Dark Matter

Article title: “Absorption of light dark matter in semiconductors”

Authors: Yonit Hochberg, Tongyan Lin, and Kathryn M. Zurek

Reference: arXiv:1608.01994

Direct detection strategies for dark matter (DM) have grown significantly from the dominant narrative of looking for scattering of these ghostly particles off of large and heavy nuclei. Such experiments involve searches for the Weakly-Interacting Massive Particles (WIMPs) in the many GeV (gigaelectronvolt) mass range. Such candidates for DM are predicted by many beyond Standard Model (SM) theories, one of the most popular involving a very special and unique extension called supersymmetry. Once dubbed the “WIMP Miracle”, these types of particles were found to possess just the right properties to be suitable as dark matter. However, as these experiments become more and more sensitive, the null results put a lot of stress on their feasibility.

Typical detectors like that of LUX, XENON, PandaX and ZEPLIN, detect flashes of light (scintillation) from the result of particle collisions in noble liquids like argon or xenon. Other cryogenic-type detectors, used in experiments like CDMS, cool semiconductor arrays down to very low temperatures to search for ionization and phonon (quantized lattice vibration) production in crystals. Already incredibly successful at deriving direct detection limits for heavy dark matter, new ideas are emerging to look into the lighter side.

Recently, DM below the GeV range have become the new target of a huge range of detection methods, utilizing new techniques and functional materials – semiconductors, superconductors and even superfluid helium. In such a situation, recoils from the much lighter electrons in fact become much more sensitive than those of such large and heavy nuclear targets.

There are several ways that one can consider light dark matter interacting with electrons. One popular consideration is to introduce a new gauge boson that has a very small ‘kinetic’ mixing with the ordinary photon of the Standard Model. If massive, these ‘dark photons’ could also be potentially dark matter candidates themselves and an interesting avenue for new physics. The specifics of their interaction with the electron are then determined by the mass of the dark photon and the strength of its mixing with the SM photon.

Typically the gap between the valence and conduction bands in semiconductors like silicon and germanium is around an electronvolt (eV). When the energy of the dark matter particle exceeds the band gap, electron excitations in the material can usually be detected through a complicated secondary cascade of electron-hole pair generation. Below the band gap however, there is not enough energy to excite the electron to the conduction band, and so detection proceeds through low-energy multi-phonon excitations, with the dominant being the emission of two back-to-back phonons.

In both these regimes, the absorption rate of dark matter in the material is directly related to the properties of the material, namely its optical properties. In particular, the absorption rate for ordinary SM photons is determined by the polarization tensor in the medium, and in turn the complex conductivity, \hat{\sigma}(\omega)=\sigma_{1}+i \sigma_{2} , through what is known as the optical theorem. Ultimately this describes the response of the material to an electromagnetic field, which has been measured in several energy ranges. This ties together the astrophysical properties of how the dark matter moves through space and the fundamental description of DM-electron interactions at the particle level.

In a more technical sense, the rate of DM absorption, in events per unit time per unit target mass, is given by the following equation:

R=\frac{1}{\rho} \frac{\rho_{D M}}{m_{A^{\prime}}} \kappa_{e f f}^{2} \sigma_{1}

  • \rho – mass density of the target material
  • \rho_{DM} – local dark matter mass density (0.3 GeV/cm3) in the galactic halo
  • m_{A'} – mass of the dark photon particle
  • \kappa_{eff} – kinetic mixing parameter (in-medium)
  • \sigma_1 – absorption rate of ordinary SM photons

Shown in Figure 1, the projected sensitivity at 90% confidence limit (C.L.) for a 1 kg-year exposure of semiconductor target to dark photon detection can be almost an order of magnitude greater than existing nuclear recoil experiments. Dependence is shown on the kinetic mixing parameter and the mass of the dark photon. Limits are also shown for existing semiconductor experiments, known as DAMIC and CDMSLite with 0.6 and 70 kg-day exposure, respectively.

Figure 1. Projected reach of a silicon (blue, solid) and germanium (green, solid) semiconductor target at 90% C.L. for 1 kg-year exposure through the absorption of dark photons DM, kinetically mixed with SM photons. Multi-phonon excitations are significant for the sub-eV range, and electron excitations approximately over 0.6 and 1 eV (the size of the band gaps for germanium and silicon, respectively).

Furthermore, in the millielectronvolt-kiloelectronvolt range, these could provide much stronger constraints than any of those that currently exist from sources in astrophysics, even at this exposure. These materials also provide a novel way of detecting DM in a single experiment, so long as improvements are made in phonon detection.

These possibilities, amongst a plethora of other detection materials and strategies, can open up a significant area of parameter space for finally closing in on the identity of the ever-elusive dark matter!

References and further reading: 

Posted on

Cosmic Microwave Background: The Role of Particles in Astrophysics

Over the past decade, a new trend has been emerging in physics, one that is motivated by several key questions: what do we know about the origin of our universe? What do we know about its composition? And how will the universe evolve from here? To delve into these questions naturally requires a thorough examination of the universe via the astrophysics lens. But studying the universe on a large scale alone does not provide a complete picture. In fact, it is just as important to see the universe on the smallest possible scales, necessitating the trendy and (fairly) new hybrid field of particle astrophysics. In this post, we will look specifically at the cosmic microwave background (CMB), classically known as a pillar of astrophysics, within the context of particle physics, providing a better understanding of the broader questions that encompass both fields.

Essentially, the CMB is just what we see when we look into the sky and we aren’t looking at anything else. Okay, fine. But if we’re not looking at something in particular, why do we see anything at all? The answer requires us to jump back a few billion years to the very early universe.

Particle interactions shown up to point of recombination, after which photon paths are unchanged.
Figure 1: Particle interactions shown up to point of recombination, after which photon paths are unchanged.

Immediately after the Big Bang, it was impossible for particles to form atoms without immediately being broken apart by constant bombardment from stray photons. About 380,000 thousand years after the Big Bang, the Universe expanded and cooled to a temperature of about 3,000 K, allowing the first formation of stable hydrogen atoms. Since hydrogen is electrically neutral, the leftover photons could no longer interact, meaning that at that point their paths would remain unaltered indefinitely. These are the photons that we observe as CMB; Figure 1 shows this idea diagrammatically below. From our present observation point, we measure the CMB to have a temperature of about 2.76 K.

Since this radiation has been unimpeded since that specific point (known as the point of ‘recombination’), we can think of the CMB as a snapshot of the very early universe. It is interesting, then, to examine the regularity of the spectrum; the CMB is naturally not perfectly uniform, and the slight temperature variations can provide a lot of information about how the universe formed. In the early primordial soup universe, slight random density fluctuations exerted a greater gravitational pull on their surroundings, since they had slightly more mass. This process continues, and very large dense patches occur in an otherwise uniform space, heating up the photons in that area accordingly. The Planck satellite, launched in 2009, provides some beautiful images of the temperature anisotropies of the universe, as seen in Figure 2. Some of these variations can be quite severe, as in the recently released results about a supervoid aligned with an especially cold spot in the CMB (see Further Reading, item 4).

 

Planck satellite heat map images of the CMB.
Figure 2: Planck satellite heat map images of the CMB.

 

Composition of the universe by percent.
Figure 3: Composition of the universe by percent.

So what does this all have to do with particles? We’ve talked about a lot of astrophysics so far, so let’s tie it all together. The big correlation here is dark matter. The CMB has given us strong evidence that our universe has a flat geometry, and from general relativity, this provides restrictions on the mass, energy, and density of the universe. In this way, we know that atomic matter can constitute only 5% of the universe, and analysis of the peaks in the CMB gives an estimate of 26% for the total dark matter presence. The rest of the universe is believed to be dark energy (see Figure 3).

Both dark matter and dark energy are huge questions in particle physics that could be the subject of a whole other post. But the CMB plays a big role in making our questions a bit more precise. The CMB is one of several pieces of strong evidence that require the existence of dark matter and dark energy to justify what we observe in the universe. Some potential dark matter candidates include weakly interacting massive particles (WIMPs), sterile neutrinos, or the lightest supersymmetric particle, all of which bring us back to particle physics for experimentation. Dark energy is not as well understood, and there are still a wide variety of disparate theories to explain its true identity. But it is clear that the future of particle physics will likely be closely tied to astrophysics, so as a particle physicist it’s wise to keep an eye out for new developments in both fields!

 

Further Reading: 

  1. “The Cosmic Cocktail: Three Parts Dark Matter”, Katherine Freese
  2. “Physics of the cosmic microwave background anistropy”, from the arXiv:astro-ph
  3. Summary of dark matter vs. dark energy and other resources from NASA
  4. Summary of the supervoid aligned with a cold spot in the CMB, Royal Astronomical Society monthly notices