2022 saw the pandemic-delayed Snowmass process confront the past, present, and future of particle physics. As the last papers trickle in for the year, we review Snowmass’s major developments and takeaways for particle theory.

It’s February 2022, and I am in an auditorium next to the beach in sunny Santa Barbara, listening to particle theory experts discuss their specialty. Each talk begins with roughly the same starting point: the Standard Model (SM) is incomplete. We know it is incomplete because, while its predictive capability is astonishingly impressive, it does not address a multitude of puzzles. These are the questions most familiar to any reader of popular physics: What is dark matter? What is dark energy? How can gravity be incorporated into the SM, which describes only 3 of the 4 known fundamental forces? How can we understand the origin of the SM’s structure — the values of its parameters, the hierarchy of its scales, and its “unnatural” constants that are calculated to be mysteriously small or far too large to be compatible with observation? 

This compilation of questions is the reason that I, and all others in the room, are here. In the 80s, the business of particle discovery was booming. Eight new particles had been confirmed in the past two decades alone, cosmology was pivoting toward the recently developed inflationary paradigm, and supersymmetry (SUSY) was — as the lore goes — just around the corner. This flourish of progress and activity in the field had become too extensive for any collaboration or laboratory to address on its own. Meanwhile, links between theoretical developments, experimental proposals, and the flurry of results ballooned. The transition from the solitary 18th century tinkerer to the CERN summer student running an esoteric simulation for a research group was now complete: particle physics, as a field and community, had emerged. 

It was only natural that the field sought a collective vision, or at minimum a notion of promising directions to pursue. In 1982, the American Physical Society’s Division of Particles and Fields organized Snowmass, a conference of a mere hundred participants that took place in a single room on a mountain in its namesake town of Snowmass, Colorado. Now, too large to be contained by its original location (although enthusiasm for organizing physics meetings at prominent ski locations abounds), Snowmass is both a conference and a multi-year process. 

The depth and breadth of particle physics knowledge acquired in the last half-century is remarkable, yet a snapshot of the field today appears starkly different. The Higgs boson just celebrated its tenth “discovery birthday”, and while the completion of the Standard Model (SM) as we know it is no doubt a momentous achievement, no new fundamental particles have been found since, despite overwhelming evidence of the inevitability of new physics. Supersymmetry may still prove to be just around the corner at a next-generation collider…or orders of magnitude beyond our current experimental reach. Despite attention-grabbing headlines that herald the “death” of particle physics, there remains an abundance of questions ripe for exploration. 

In light of this shift, the field is up against a challenge: how do we reconcile the disappointments of supersymmetry? Moreover, how can we make the case for the importance of fundamental physics research in an increasingly uncertain landscape?

The researchers are here at the Kavli Institute for Theoretical Physics (KITP) at UC Santa Barbara to map out the “Theory Frontier” of the Snowmass process. The “frontiers” — subsections of the field focusing on a different approach of particle physics — have met over the past year to weave their own story of the last decade’s progress, burgeoning both questions and promising future trajectories. This past summer, thousands of particle physicists across the frontiers convened in Seattle, Washington to share, debate, and ponder questions and new directions. Now, these frontiers are collating their stories into an anthology. 

Below are a few (theory) focal points in this astoundingly expansive picture.

Scattering Amplitudes

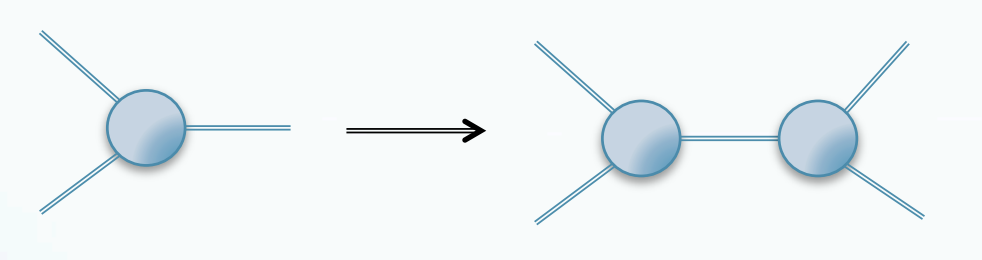
Quantum field theory (QFT) is the common language of particle physics. QFT provides a description of a particle system based on two fundamental tools: the Lagrangian and the path integral, which can both be wrapped up in the familiar diagrams of Richard Feynman. This approach, utilizing a visualization of incoming and outgoing scattering or decaying particles, has provided relief to many Ph.D. students over the past few generations due to its comparative ease of use. The diagrams are roughly divided into three parts: propagators (which tell us about the motion of a free particle), vertices (in which three or more particles interact), and loops (which describe the scenario in which the trajectory of two particles form a closed path). They contain both real, incoming particles, which are known as on-shell, as well as virtual, intermediate particles that cannot be measured, which are known as off-shell. To calculate a scattering amplitude — the probability of one or more particles interacting to form some specified final state — in this paradigm requires summing over all possibilities of what these virtual particles may be. This can prove not only cumbersome, but can also result in redundancies in our calculations.

Particle theory, however, is undergoing a paradigm shift. If we instead focus on the physical observable itself, the scattering amplitude, we can build more complicated diagrams from simpler ones in a recursive fashion. For example, we can imagine creating a 4-particle amplitude by gluing together two 3-particle amplitudes, as shown above. The process bypasses the intermediate, virtual particles and focuses only on computing on-shell states. This is not only a nice feature, but it can significantly reduce the problem at hand: calculating the scattering amplitude of 8 gluons with the Feynman approach  requires computing more than a million Feynman diagrams, whereas the amplitudes method reduces the problem to a mere half-line. 

In recent years, this program has seen renewed efforts, not only for its practical simplicity but also for its insights into the underlying concepts that shape particle interactions. The Lagrangian formalism organizes a theory based on the fields it contains and the symmetries those fields obey, with the rule of thumb that any term respecting the theory’s symmetries can be included in the Lagrangian. Further, these terms satisfy several general principles: Unitarity (the sum of the probabilities of each possible process in the theory adds to one, and time-evolves in a respecting manner), causality (an effect originates only from a cause that is contained in the effect’s backward light cone), and locality (observables that are localized at distinct regions in spacetime cannot affect one another). These are all reasonable axioms, but they must be explicitly baked into a theory that is represented in the Lagrangian formalism. Scattering amplitudes, in contrast, can reveal these principles without prior assumptions, signaling the unveiling of a more fundamental structure.

Recent research surrounding amplitudes concerns both diving deeper into this structure, as well as applying the results of the amplitudes program toward precision theory predictions. The past decade has seen a flurry of results from an idea known as bootstrapping, which takes the relationship between physics and mathematics and flips it on its head.

QFTs are typically built up from “bottom-up” by including terms in the Lagrangian based on which fields are present and which symmetries they obey. The bootstrapping methodology instead asks what the observable quantities are that result from a theory, and considers which underlying properties they must obey in order to be mathematically consistent. This process of elimination rules out a large swath of possibilities, significantly constraining the system and allowing us to, in some cases, guess our way to the answer. 

This rich research program has plenty of directions to pursue. We can compute the scattering amplitudes of multi-loop diagrams in order to arrive at extremely precise SM predictions. We can probe their structure in the classical regime with the gravitational waves resulting from inspiraling stellar and black hole binaries. We can apply them to less understood regimes; for example, cosmological scattering amplitudes pose a unique challenge because they proceed in curved, rather than flat, space. Are there curved space analogues to the flat space amplitude structures? If so, what are they? What can we compute with them? Amplitudes are pushing forward our notion of what a QFT is. With them, we may be able to uncover the more fundamental frameworks that must underlie particle physics.

Computational Advances

Making theoretical predictions in the modern era has become incredibly computationally expensive. The Large Hadron Collider (LHC) and other accelerators produce over 100 terabytes of data per day while running, requiring not only intensive data filtering systems, but efficient computational methods to categorize and search for the signatures of particle collisions. Performing calculations in the quark sector — which relies on lattice gauge theory, in which spacetime is broken down into a discrete grid — also requires vast computational resources. And as simulations in astrophysics and cosmology balloon, so too does the supercomputing power needed to handle them. 

This challenge over the past decade has received a significant helping hand from the advent of machine learning — deep learning in particular. On the collider front, these techniques have been applied to the detection of anomalies — a deviation in the data from the SM “background” that may signal new physics — as well as the analysis of jets. These protocols can be trained on previously analyzed collider data and synthetic data to establish benchmarks and push computational efficiency much further. As the LHC enters its third operational run, it will be particularly focused on precision measurements as the increasing quantity of data allows for higher statistical certainty in our results. The growing list of anomalies — including the W mass measurement and the muon g-2 anomaly — will confront these increased statistics, allowing for possible confirmation or rejection of previous results. Our analyses have also grown more sophisticated; the showers of quarks and gluons that result from collisions of hadrons known as jets have proved to reveal substructure that opens up another avenue for comparison of data with an SM theory prediction. 

The quark sector especially will benefit from the growing adoption of machine learning in particle physics. Analytical calculations in this sector are intractable due to strong coupling, so in practice calculations are built upon the use of lattice gauge theory. Increasingly precise calculations are dependent upon making this grid smaller and smaller and including more and more particles. 

As physics continually benefits from the rapid development of machine learning and artificial intelligence, the field is up against a unique challenge. Machine learning algorithms can often be applied blindly, resulting in misunderstood outputs via a black box. The key in utilizing these techniques effectively is in asking the right questions, understanding what questions we are asking, and translating the physics appropriately to a machine learning context. This has its practical uses — in confidently identifying tasks for which automation is appropriate — but also opens up the possibility to formulate theoretical particle physics in a computational language. As we look toward the future, we can dream of the possibilities that could result from such a language: to what extent can we train a machine to learn physics itself? There is much work to be done before such questions can be answered, but the prospects are exciting nonetheless.

Cosmological Approaches

As the promise of SUSY is so far unfilled, the space of possible models is expansive, and anomalies pop up and disappear in our experiments, the field is yearning for a source of new data. While colliders have fueled significant progress in the past decades, a new horizon has formed with the launching of ultra-precise telescopes and gravitational wave detectors: probing the universe via cosmological data. 

The use of observations of astrophysical and cosmological sources to tell us about particle physics is not new, — we’ve long hunted for supernovae and mapped the cosmic microwave background (CMB) — but nascent theory developments hold incredible potential for discovery. As of 2015, observations of gravitational waves guide insights into stellar and black hole binaries, with an eye toward a detection of a stochastic gravitational wave background originating from the period of exponential expansion known as inflation, which proceeded shortly after the big bang. The observation of black hole binaries in particular can provide valuable insights into the workings of gravity at the smallest of scales, when it enters the realm of quantum mechanics. The possibility of a stochastic gravitational wave background raises the promise of “seeing” the workings of the universe at earlier stages in its history than we’ve ever before been able to access, potentially even to the start of the universe itself. 

Inflation also lends itself to other applications within particle physics. Quantum fields at the beginning of the universe, in alignment with the uncertainty principle, predict tiny, statistical fluctuations. These initial spacetime curvature perturbations beget density perturbations in the distribution of matter which beget the temperature fluctuations visible in the cosmic microwave background (CMB). These fluctuations are observed to be distributed according to a Gaussian normal distribution, as of the latest CMB datasets. But tiny, primordial non-Gaussianities — processes that lead to a correlated pattern of fluctuations in the CMB and other datasets — are predicted for certain particle interactions during inflation. In particular, if particles interacting with the fields responsible for inflation acquire heavy masses during inflation, they could imprint a distinct, oscillating signature within these datasets. This would show up in our observables, such as the large-scale distribution of galaxies shown above, in the form of triangular (or higher-point polygonal) shapes signaling a non-Gaussian correlation. Currently, our probes of these non-Gaussianities are not precise enough to unveil such signatures, but planned and upcoming experiments may establish this new window into the workings of the early universe. 

Finally, a section on the intersections of cosmology and particle physics would not be complete without mention of everyone’s favorite mystery: dark matter. A decade ago, the prime candidate for dark matter was the WIMP — the Weakly Interacting Massive Particle. This model was fairly simple, able to account for the 25% dark matter content of the universe we observe today, and remain in harmony with all other known cosmology. However, we’ve now probed a large swath of possible masses and cross-sections for the WIMP and come up short. The field’s focus has shifted to a different candidate for dark matter, the axion, which addresses both the dark matter mystery and a puzzle known as the strong CP problem simultaneously. While experiments to probe the axion parameter space are built, theorists are tasked with identifying well-motivated regions of this space — that is, possibilities for the mass and other parameters describing the axion that are plausible. The prospects include: theoretical motivation from calculations in string theory, considerations of the Peccei-Quinn symmetry underlying the notion of an axion, as well as various possible modes of production, including extreme astrophysical environments such as neutron stars and black holes. 

Cosmological data has thus far been an important source not only into the history and evolution of the universe, but also of particle physics at high energy scales. As new telescopes and gravitational wave observatories are slated to come online within the next decade, expect this prolific field to continue to deliver alluring prospects for physics beyond the SM.

Neutrinos

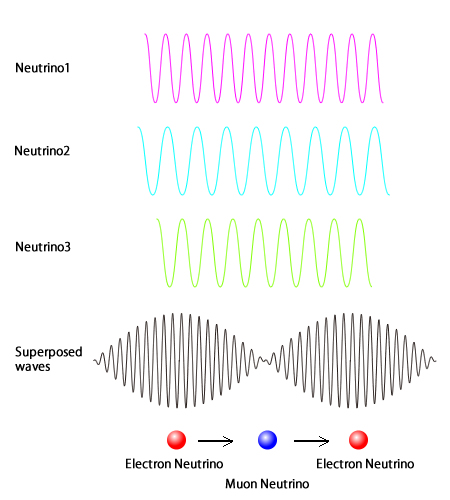
While the previous sections have highlighted new approaches to uncovering physics beyond the SM, there is a particular collection of particles that stand out in the spotlight. In the SM formulation, the three flavors of neutrinos are massless, just like the photon. Yet we know unequivocally from experiment that this is false. Neutrinos display a phenomenon known as neutrino mixing, in which one flavor of neutrino can turn into another flavor of neutrino as it propagates. This implies that at least two of the three neutrino flavors are in fact massive

Investigating why neutrinos have mass — and where that mass comes from — is a central question in particle physics. Neutrinos are especially captivating because any observation of a neutrino mass mechanism is guaranteed to be a window to new physics. Further, neutrinos could be of central importance to several puzzles within the SM, including the MicroBooNE anomaly, the question of why there is more matter than antimatter in the observable universe, and the flavor puzzle, among others. The latter refers to an overall lack of understanding of the origin of flavor in the SM. Why do quarks come in six flavors, organized into three generations each consisting of one “up-type” quark with a +⅔ charge and one “down-type” quarks with a -⅓ charge? Why do leptons come in six flavors, with three pairs of one electron-like particle and one neutrino? What is the origin of the hierarchy of masses for both quarks and leptons? Of the SM’s 19 free parameters — which includes particle masses, coupling strengths, and others — 14 of them are associated with flavor. 

The unequivocal evidence for neutrino mixing was the crown prize of the last few decades of neutrino physics research. Modern experiments are charged with detecting more subtle signs of new physics, through measurements of neutrino energy in colliders, ever more precise oscillation data, and the possibility for a heavy neutrino belonging to a fourth generation. 

Experiment has a clear role to play; the upcoming Deep Underground Neutrino Experiment (DUNE) will produce neutrinos at Fermilab and observe them at Sanford Lab, South Dakota in order to accumulate data regarding long-distance neutrino oscillation. DUNE and other detectors will also turn their eye toward the sky in observations of neutrinos sourced by supernovae. There is also much room for theorists, both in developing models for neutrino mass-generation as well as influencing the future of neutrino experiment — short-distance neutrino oscillation experiments are a key proposal in the quest to address the MicroBooNE anomaly. 

The field of neutrino physics is only growing. It is likely we’ll learn much more about the SM and beyond through these ghostly, mysterious particles in the coming decades.

Which Collider(s)?

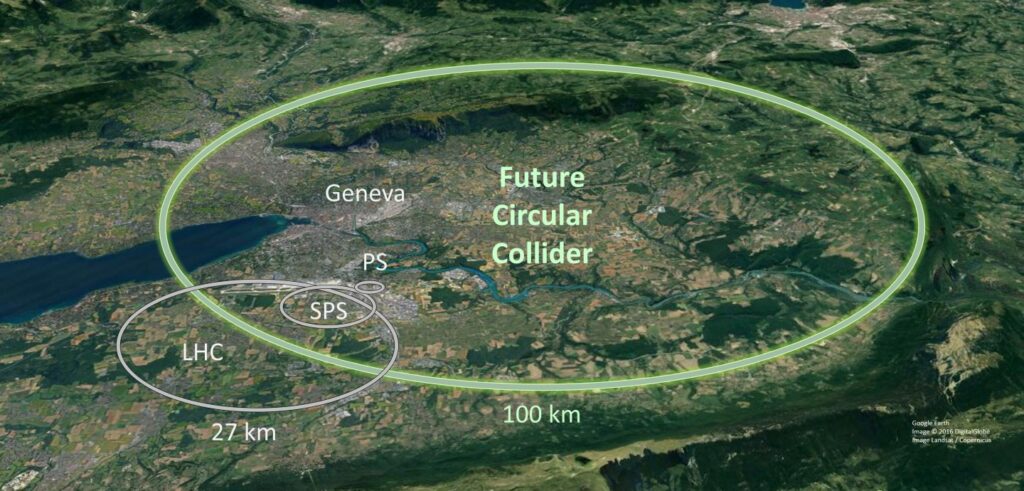
One looming question has formed an undercurrent through the entirety of the Snowmass process: What’s next after the LHC? In the past decade, propositions have been fleshed out in various stages, with the goal of satisfying some part of the lengthy wish list of questions a future collider would hope to probe. 

The most well-known possible successor to the LHC is the Future Circular Collider (FCC), which is roughly a plan for a larger LHC, able to reach energies some 30 times that of its modern-day counterpart. An FCC that collides hadrons, as the LHC does, would extend the reach of our studies into the Higgs boson, other force-carrying gauge bosons, and dark matter searches. Its higher collision rate would enable studies of rare hadron decays and continue the trek into the realm of flavor physics searches. It would also enable our discovery of gauge bosons of new interactions — if they exist at those energies. This proposal, while captivating, has also met its fair share of skepticism, particularly because there is no singular particle physics goal it would be guaranteed to achieve. When the LHC was built, physicists were nearly certain that the Higgs boson would be found there — and it was. However, physicists were also somewhat confident in the prospect of finding SUSY at the LHC. Could supersymmetric particles be discovered at the FCC? Maybe, or maybe not. 

A second plan exists for the FCC, in which it collides electrons and positrons instead of hadrons. This targets the electroweak sector of the SM, covering the properties of the Higgs, the W and Z bosons, and the heaviest quark (the top quark). Whereas hadrons are composite particles, and produce particle showers and jets upon collision, leptons are fundamental particles, and so have well-defined initial states. This allows for greater precision in measurements compared to hadron colliders, particularly in questions of the Higgs. Is the Higgs boson the only Higgs-like particle? Is it a composite particle? How does the origin of mass influence other key questions, such as the nature of dark matter? While unable to reach as high of energies as a hadron collider, an electron-positron collider is appealing due to its precision. This dichotomy epitomizes the choice between these two proposals for the FCC.

The options go beyond circular colliders. Linear colliders such as the International Linear Collider (ILC) and Compact Linear Collider (CLIC) are also on the table. While circular colliders are advantageous for their ability to accelerate particles over long distances and to keep un-collided particles in circulation for other experiments, they come with a particular disadvantage due to their shape. The acceleration of charged particles along a curved path results in synchrotron radiation — electromagnetic radiation that significantly reduces the energy available for each collision. For this reason, a circular accelerator is more suited to the collision of heavy particles — like the protons used in the LHC — than much lighter leptons. The lepton collisions within a linear accelerator would produce Higgs bosons at a high rate, allowing for deeper insight into the multitude of Higgs-related questions.

In the past few years, interest has grown for a different kind of lepton collider: a muon collider. Muons are, like electrons, fundamental particles, and therefore much cleaner in collisions than composite hadrons. They are also much more massive than electrons, which leads to a smaller proportion of energy being lost to synchrotron radiation in comparison to electron-positron colliders. This would allow for both high-precision measurements as well as high energies, making a muon collider an incredibly attractive candidate. The heavier mass of the muon, however, does bring with it a new set of technical challenges, particularly because the muon is not a stable particle and decays within a short timeframe. 

As a multi-billion dollar project requiring the cooperation of numerous countries, getting a collider funded, constructed, and running is no easy feat. As collider proposals are put forth and debated, there is much at stake — a future collider will also determine the research programs and careers of many future students and professors. With that in mind, considerable care is necessary. Only one thing is certain: there will be something after the LHC.

Toward the Next Snowmass

The above snapshots are only a few of the myriad subtopics within particle theory; other notable ones include string theory, quantum information science, lattice gauge theory, and effective field theory. The full list of contributed papers can be found here. 

As the Snowmass process wraps up, the voice of particle theory has played and continues to play an influential role. Overall, progress in theory remains more accessible than in experiment —  the number of possible models we’ve developed far outpaces the detectors we are able to build to investigate them. The theoretical physics community both guides the direction and targets of future experiments, and has plenty of room to make progress on the model-building front, including understanding quantum field theories at the deepest level and further uncovering the structures of amplitudes. A decade ago, SUSY at LHC-scales was at the prime objective in the hunt for an ultimate theory of physics. Now, new physics could be anywhere and everywhere; Snowmass is crucial to charting our path in an endless valley of questions. I look forward to the trails of the next decade.

Title: “Search for an Excess of Electron Neutrino Interactions in MicroBooNE Using Multiple Final State Topologies”

Authors: MicroBooNE Collaboration

References: https://arxiv.org/pdf/2110.14054.pdf

This is the second post in a series on the latest MicroBooNE results, covering the theory side. Click here to read about the experimental side. 

Few stories in physics are as convoluted as the one written by neutrinos. These ghost-like particles, a notoriously slippery experimental target and one of the least-understood components of the Standard Model, are making their latest splash in the scientific community through MicroBooNE, an experiment at FermiLab that unveiled its first round of data earlier this month. While MicroBooNE’s predecessors have provided hints of a possible anomaly within the neutrino sector, its own detectors have yet to uncover a similar signal. Physicists were hopeful that MicroBooNE would validate this discrepancy, yet the tale is turning out to be much more nuanced than previously thought.

Unexpected Foundations

Originally proposed by Wolfgang Pauli in 1930 as an explanation for missing momentum in certain particle collisions, the neutrino was added to the Standard Model as a massless particle that can come in one of three possible flavors: electron, muon, and tau. At first, it was thought that these flavors are completely distinct from one another. Yet when experiments aimed to detect a particular neutrino type, they consistently measured a discrepancy from their prediction. A peculiar idea known as neutrino oscillation presented a possible explanation: perhaps, instead of propagating as a singular flavor, a neutrino switches between flavors as it travels through space. 

This interpretation emerges fortuitously if the model is modified to give the neutrinos mass. In quantum mechanics, a particle’s mass eigenstate — the possible masses a particle can be found to have upon measurement — can be thought of as a traveling wave with a certain frequency. If the three possible mass eigenstates of the neutrino are different, meaning that at most one of the mass values could be zero, this creates a phase shift between the waves as they travel. It turns out that the flavor eigenstates — describing which of the electron, muon, or tau flavors the neutrino is measured to possess — are then superpositions of these mass eigenstates. As the neutrino propagates, the relative phase between the mass waves varies such that when the flavor is measured, the final superposition could be different from the initial one, explaining how the flavor can change. In this way, the mass eigenstates and the flavor eigenstates of neutrinos are said to “mix,” and we can mathematically characterize this model via mixing parameters that encode the mass content of each flavor eigenstate.

These massive oscillating neutrinos represent a radical departure from the picture originally painted by the Standard Model, requiring a revision in our theoretical understanding. The oscillation phenomenon also poses a unique experimental challenge, as it is especially difficult to unravel the relationships between neutrino flavors and masses. Thus far, physicists have only been able to determine the sum of neutrino masses, and have found that this value is constrained to be exceedingly small, posing yet another mystery. The neutrino experiments of the past three decades have set their sights on measuring the mixing parameters in order to determine the probabilities of the possible flavor switches.

A Series of Perplexing Experiments

In 1993, scientists in Los Alamos peered at the data gathered by the Liquid Scintillator Neutrino Detector (LSND) to find something rather strange. The group had set out to measure the number of electron neutrino events produced via decays in their detector, and found that this number exceeded what had been predicted by the three-neutrino oscillation model. In 2002, experimentalists turned on the complementary MiniBooNE detector at FermiLab (BooNE is an acronym for Booster Neutrino Experiment), which searched for oscillations of muon neutrinos into electron neutrinos, and again found excess electron neutrino events. For a more detailed account of the setup of these experiments, check out Oz Amram’s latest piece.

While two experiments are notable for detecting excess signal, they stand as outliers when we consider all neutrino experiments that have collected oscillation data. Collaborations that were taking data at the same time as LSND and MiniBooNE include: MINOS (Main Injector Neutrino Oscillation Search), KamLAND (Kamioka Liquid Scintillator Antineutrino Detector), and IceCube (surprisingly, not a fancy acronym, but deriving its name from the fact that it’s located under ice in Antarctica), to name just a few prominent ones. Their detectors targeted neutrinos from a beamline, nearby nuclear reactors, and astrophysical sources, respectively. Not one found a mismatch between predicted and measured events. 

The results of these other experiments, however, do not negate the findings of LSND and MiniBooNE. This extensive experimental range — probing several sources of neutrinos, and detecting with different hardware specifications — is necessary in order to consider the full range of possible neutrino mixing parameters and masses. Each model or experiment is endowed with a parameter space: a set of allowed values that its parameters can take. In this case, the neutrino mass and mixing parameters form a two-dimensional grid of possibilities. The job of a theorist is to find a solution that both resolves the discrepancy and has a parameter space that overlaps with allowed experimental parameters. Since LSND and MiniBooNE had shared regions of parameter space, the resolution of this mystery should be able to explain not only the origins of the excess, but why no similar excess was uncovered by other detectors.

A simple explanation to the anomaly emerged and quickly gained traction: perhaps the data hinted at a fourth type of neutrino. Following the logic of the three-neutrino oscillation model, this interpretation considers the possibility that the three known flavors have some probability of oscillating into an additional fourth flavor. For this theory to remain consistent with previous experiments, the fourth neutrino would have to provide the LSND and MiniBooNE excess signals, while at the same time sidestepping prior detection by coupling to only the force of gravity. Due to its evasive behavior, this potential fourth neutrino has come to be known as the sterile neutrino. 

The Rise of the Sterile Neutrino

The sterile neutrino is a well-motivated and especially attractive candidate for beyond the Standard Model physics. It differs from ordinary neutrinos, also called active neutrinos, by having the opposite “handedness”. To illustrate this property, imagine a spinning particle. If the particle is spinning with a leftward orientation, we say it is “left-handed”, and if it is spinning with a rightward orientation, we say it is “right-handed”. Mathematically, this quantity is called helicity, which is formally the projection of a particle’s spin along its direction of momentum. However, this helicity depends implicitly on the reference frame from which we make the observation. Because massive particles move slower than the speed of light, we can choose a frame of reference such that the particle appears to have momentum going in the opposite direction, and as a result, the opposite helicity. Conversely, because massless particles move at the speed of light, they will have the same helicity in every reference frame. 

This frame-dependence unnecessarily complicates calculations, but luckily we can instead employ a related quantity that encapsulates the same properties while bypassing the reference frame issue: chirality. Much like helicity, while massless particles can only display one chirality, massive particles can be either left- or right-chiral. Neutrinos interact via the weak force, which is famously parity-violating, meaning that it has been observed to preferentially interact only with particles of one particular chirality. Yet massive neutrinos could presumably also be right-handed — there’s no compelling reason to think they shouldn’t exist. Sterile neutrinos could fill this gap.

They would also lend themselves nicely to addressing questions of dark matter and baryon asymmetry. The former — the observed excess of gravitationally-interacting matter over light-emitting matter by a factor of 20 — could be neatly explained away by the detection of a particle that interacts only gravitationally, much like the sterile neutrino. The latter, in which our patch of the universe appears to contain considerably more matter than antimatter, could also be addressed by the sterile neutrino via a proposed model of neutrino mass acquisition known as the seesaw mechanism. 

In this scheme, active neutrinos are represented as Dirac fermions: spin-½ particles that have a unique anti-particle, the oppositely-charged particle with otherwise the same properties. In contrast, sterile neutrinos are considered to be Majorana fermions: spin-½ particles that are their own antiparticle. The masses of the active and sterile neutrinos are fundamentally linked such that as the value of one goes up, the value of the other goes down, much like a seesaw. If sterile neutrinos are sufficiently heavy, this mechanism could explain the origin of neutrino masses and possibly even why the masses of the active neutrinos are so small. 

These considerations position the sterile neutrino as an especially promising contender to address a host of Standard Model puzzles. Yet it is not the only possible solution to the LSND/MiniBooNE anomaly — a variety of alternative theoretical interpretations invoke dark matter, variations on the Higgs boson, and even more complicated iterations of the sterile neutrino. MicroBooNE was constructed to traverse this range of scenarios and their corresponding signatures. 

Open Questions

After taking data for three years, the collaboration has compiled two dedicated analyses: one that searches for single electron final states, and another that searches for single photon final states. Each of these products can result from electron neutrino interactions — yet both analyses did not detect an excess, pointing to no obvious signs of new physics via these channels. 

Although confounding, this does not spell death for the sterile neutrino. A significant disparity between MiniBooNE and MicroBooNE’s detectors is the ability to discern between single and multiple electron events — MiniBooNE lacked the resolution that MicroBooNE was upgraded to achieve. MiniBooNE also was unable to fully distinguish between electron and photon events in the same way as MicroBooNE. The possibility remains that there exist processes involving new physics that were captured by LSND and MiniBooNE — perhaps decays resulting in two electrons, for instance.  

The idea of a right-handed neutrino remains a promising avenue for beyond the Standard Model physics, and it could turn out to have a mass much larger than our current detection mechanisms can probe. The MicroBooNE collaboration has not yet done a targeted study of the sterile neutrino, which is necessary in order to fully assess how their data connects to its possible signatures. There still exist regions of parameter space where the sterile neutrino could theoretically live, but with every excluded region of parameter space, it becomes harder to construct a theory with a sterile neutrino that is consistent with experimental constraints. 

While the list of neutrino-based mysteries only seems to grow with MicroBooNE’s latest findings, there are plenty of results on the horizon that could add clarity to the picture. Researchers are anticipating the output of more data from MicroBooNE as well as more specific theoretical studies of the results and their relationship to the LSND/MiniBooNE anomaly, the sterile neutrino, and other beyond the Standard Model scenarios. MicroBooNE is also just one in a series of planned neutrino experiments, and will operate alongside the upcoming SBND (Short-Baseline Neutrino Detector) and ICARUS (Imaging Cosmic Rare and Underground Signals), further expanding the parameter space we are able to probe.

The neutrino sector has proven to be fertile ground for physics beyond the Standard Model, and it is likely that this story will continue to produce more twists and turns. While we have some promising theoretical explanations, nothing theorists have concocted thus far has fit seamlessly with our available data. More data from MicroBooNE and near-future detectors is necessary to expand our understanding of these puzzling pieces of particle physics. The neutrino story is pivotal to the tome of the Standard Model, and may be the key to writing the next chapter in our understanding of the fundamental ingredients of our world.

Further Reading

1. A review of neutrino oscillation and mass properties: https://pdg.lbl.gov/2020/reviews/rpp2020-rev-neutrino-mixing.pdf
2. An in-depth review of the LSND and MiniBooNE results: https://arxiv.org/pdf/1306.6494.pdf

This is post #1 of a three-part series on the Muon g-2 experiment.

April 7th is an eagerly anticipated day. It recalls eagerly anticipated days of years past, which, just like the spring Wednesday one week from today, are marked with an announcement. It harkens back to the discovery of the top quark, the premier observation of tau neutrinos, or the first Higgs boson signal. There have been more than a few misfires along the way, like BICEP2’s purported gravitational wave background, but these days always beget something interesting for the future of physics, even if only an impetus to keep searching. In this case, all the hype surrounds one number: muon g-2. 

This quantity describes the anomalous magnetic dipole moment of the muon, the second-heaviest lepton after the electron, and has been the object of questioning ever since the first measured value was published at CERN in December 1961. Nearly sixty years later, the experiment has gone through a series of iterations, each seeking greater precision on its measured value in order to ascertain its difference from the theoretically-predicted value. New versions of the experiment, at CERN, Brookhaven National Laboratory, and Fermilab, seemed to point toward something unexpected: a discrepancy between the values calculated using the formalism of quantum field theory and the Muon g-2 experimental value. April 7th is an eagerly anticipated day precisely because it could confirm this suspicion. 

It would be a welcome confirmation, although certain to let loose a flock of ambulance-chasers eager to puzzle out the origins of the discrepancy (indeed, many papers are already appearing on the arXiv to hedge their bets on the announcement). Tensions between our theoretical and measured values are, one could argue, exactly what physicists are on the prowl for. We know the Standard Model (SM) is incomplete, and our job is to fill in the missing pieces, tweak the inconsistencies, and extend the model where necessary. This task prerequisites some notion of where we’re going wrong and where to look next. Where better to start than a tension between theory and experiment? Let’s dig in. 

What’s so special about the muon?

The muon is roughly 207 times heavier than the electron, but shares most of its other properties. Like the electron, it has a negative charge which we denote , and like the other leptons it is not a composite particle, meaning there are no known constituents that make up a muon. Its larger mass proves auspicious in probing physics, as this makes it particularly sensitive to the effects of virtual particles. These are not particles per se — as the name suggests, they are not strictly real — but are instead intermediate players that mediate interactions, and are represented by internal lines in Feynman diagrams like this:

Above, we can see one of the main decay channels for the muon: first the muon decays into a muon neutrino and a boson, which is one of the three bosons that mediates weak force interactions. Then, the  boson decays into an electron and electron neutrino . However, we can’t “stop” this process and observe the boson, only the final states of , , and . More precisely, this virtual particle is an excitation of the quantum field; they conserve both energy and momentum, but do not necessarily have the same mass as their real counterparts, and are essentially temporary fields.

Given the mass dependence, you could then ask why we don’t instead carry out these experiments using the tau, the even heavier cousin of the muon, and the reason for this has to do with lifetime. The muon is a short-lived particle, meaning it cannot travel long distances without decaying, but the roughly 64 microseconds of life that the accelerator gives it turns out to be enough to measure its decay products. Those products are exactly what our experiments are probing, as we would like to observe the muon’s interactions with other particles. The tau could actually be a similarly useful probe, especially as it could couple more strongly to beyond the Standard Model (BSM) physics due to its heavier mass, but we currently lack the detection capabilities for such an experiment (a few ideas are in the works).

What exactly is the anomalous magnetic dipole moment?

The “g” in “g-2” refers to a quantity called the g-factor, also known as the dimensionless magnetic moment due to its proportionality to the (dimension-ful) magnetic moment , which describes the strength of a magnetic source. This relationship for the muon can be expressed mathematically as

,

where gives the particle’s spin, e is the charge of an electron, and is the muon’s mass. Since the “anomalous” part of the anomalous magnetic dipole moment is the muon’s difference from , we further parametrize this difference by defining the anomalous magnetic dipole moment directly as

. 

Where does this difference come from?

The calculation of the anomalous magnetic dipole moment proceeds mostly through quantum electrodynamics (QED), the quantum theory of electromagnetism (which includes photon and lepton interactions), but it also gets contributions from the electroweak sector (, , Z, and Higgs boson interactions) and the hadronic sector (quark and gluon interactions). We can explicitly split up the SM value of according to each of these contributions,

.

We classify the interactions of muons with SM particles (or, more generally, between any particles) according to their order in perturbation theory. Tree-level diagrams are interactions like the decay channel in Figure 1, which involve only three-point interactions between particles and can be drawn graphically in a tree-like fashion. The next level of diagrams that contribute are at loop-level, which include an additional leg and usually, as the name suggests, contain some loop-like shape (further orders up involve multiple loops). Calculating the total probability amplitude for a given process necessitates a sum over all possible diagrams, although higher-order diagrams usually do not contribute as much and can generally (but not always) be ignored. In the case of the anomalous magnetic dipole moment, the difference between the tree-level value of comes from including the loop-level processes from fields in all the sectors outlined above. We can visualize these effects through the following loop diagrams,

In each of these diagrams, two muons decay to a photon with an internal loop of interactions in some combination of particles . From left to right: the loop is comprised of 1) two muons and a photon , 2) two muons and a boson, 3) two W bosons and a neutrino , and 4) two muons and a photon , which has some interactions involving hadrons.

Why does this value matter?

In calculating the anomalous magnetic dipole moment, we sum over all of the Feynman loop diagrams that come from known interactions, and these can be directly related to terms in our theory (formally, operators in the Lagrangian) that give rise to a magnetic moment. Working in an SM framework, this means summing over the muon’s quantum interactions with all relevant SM fields, which show up as both external and internal Feynamn diagram lines.

The current accepted experimental value is , while the SM makes a prediction of (both come with various error bars on the last 1-2 digits). Although they seem close, they differ by a factor of 3.7 (standard deviation), which is not quite the 5 threshold that physicists require to signal a discovery. Of course, this could change with next week’s announcement. Given the increased precision of the latest run of Muon g-2, these values could be confirmed up to 4 or greater, which would certainly give credence to a mismatch.

Why do the values not agree?

You’ve landed on the key question. There could be several possible explanations for the discrepancy, lying at the roots of both theory and experiment. Historically, it has not been uncommon for anomalies to ultimately be tied back to some experimental or systematic error, either having to do with instrument calibration or some statistical fluctuations. Fermilab’s latest run of Muon g-2 aims to deliver a value with a precision of 1 in 140 parts per billion, while the SM calculation yields a precision of 1 in 400 parts per billion. This means that next week, the Fermilab Muon g-2 collaboration should be able to tell us if these values agree.

On the theory side, the majority of the SM contribution to the anomalous magnetic dipole moment comes from QED, which is probably the most well-understood and well-tested sector of the SM. But there are also contributions from the electroweak and hadronic sectors — the former can also be calculated precisely, but the latter is much less understood and cannot be computed from first principles. This is due to the fact that the muon’s mass scale is also at the scale of a phenomenon known as confinement, in which quarks cannot be isolated from the hadrons that they form. This has the effect of making calculations in perturbation theory (the prescription outlined above) much more difficult. These calculations can proceed from phenomenology (having some input from experimental parameters) or from a technique called lattice QCD, in which processes in quantum chromodynamics (QCD, the theory of quarks and gluons) are done on a discretized space using various computational methods.

Lattice QCD is an active area of research and the computations are accompanied in turn by large error bars, although the last 20 years of progress in this field has refined the calculations from where they were the last time a Muon g-2 collaboration announced its results. The question as to how much wiggle room theory can provide was addressed as part of the Muon g-2 Theory Initiative, which published its results last summer and used two different techniques to calculate and verify its value for the SM theory prediction. Their methods significantly improved upon previous uncertainty estimations, meaning that although we could argue that the theory should be more understood before pursuing further avenues for an explanation of the anomaly, this holds less weight in the light these advancements.

These further avenues would be, of course, the most exciting and third possible answer to this question: that this difference signals new physics. If particles beyond the SM interacted with the muon in such a way that generated loop diagrams like the ones above, these could very well contribute to the anomalous magnetic dipole moment. Perhaps adding these contributions to the SM value would land us closer to the experimental value. In this way, we can see the incredible power of Muon g-2 as a probe: by measuring the muon’s anomalous magnetic dipole moment to a precision comparable to the SM calculation, we essentially test the completeness of the SM itself.

What could this new physics be?

There are several places we can begin to look. The first and perhaps most natural is within the realm of supersymmetry, which predicts, via a symmetry between fermions (spin-½ particles) and bosons (spin-1 particles), further particle interactions for the muon that would contribute to the value of . However, this idea probably ultimately falls short: any significant addition to would have to come from particles in the mass range of 100-500 GeV, which we have been ardently searching for at CERN, to no avail. Some still hold out hope that supersymmetry may prevail in the end, but for now, there’s simply no evidence for its existence.

Another popular alternative has to do with the “dark photon”, which is a hypothetical particle that would mix with the SM photon (the ordinary photon) and couple to charged SM particles, including the muon.  Direct searches are underway for such dark photons, although this scenario is currently disfavored, as it is conjectured that dark photons primarily decay into pairs of charged leptons. The parameter space of possibilities for its existence has been continually whittled down by experiments at BaBar and CERN.

In general, generating new physics involves inserting new degrees of freedom (fields, and hence particles) into our models. There is a vast array of BSM physics that is continually being studied. Although we have a few motivating factors for what new particles that contribute to  could be,  without sufficient underlying principles and evidence to make our case, it’s anyone’s game. A confirmation of the anomaly on April 7th would surely set off a furious search for potential solutions — however, the precision required to even quash the anomaly would in itself be a wondrous and interesting result.

How do we make these measurements?

Great question! For this I defer to our resident Muon g-2 experimental expert, Andre Sterenberg-Frankenthal, who will be posting a comprehensive answer to this question in the next few days. Stay tuned.

Further Resources:

1. Fermilab’s Muon g-2 website (where the results will be announced!): https://muon-g-2.fnal.gov/
2. More details on contributions to the anomalous magnetic dipole moment: https://pdg.lbl.gov/2019/reviews/rpp2018-rev-g-2-muon-anom-mag-moment.pdf 
3. The Muon g-2 Theory Initiative’s results in all of its 196-page glory: https://arxiv.org/pdf/2006.04822.pdf

Title: “A Strong No-Go Theorem on Wigner’s Friend Paradox.”

Author: Kok-Wei Bong et al.

Reference: https://arxiv.org/pdf/1907.05607.pdf 

There’s one thing nearly everyone in physics agrees upon: quantum theory is bizarre. Niels Bohr, one of its pioneers, famously said that “anybody who is not shocked by quantum mechanics cannot possibly have understood it.” Yet it is also undoubtedly one of the most precise theories humankind has concocted, with its intricacies continually verified in hundreds of experiments to date. It is difficult to wrap our heads around its concepts because a quantum world does not equate to human experience; our daily lives reside in the classical realm, as does our language. In introductory quantum mechanics classes, the notion of a wave function often relies on shaky verbiage: we postulate a wave function that propagates in a wavelike fashion but is detected as an infinitesimally small point object, “collapsing” upon observation. The nature of the “collapse” — how exactly a wave function collapses, or if it even does at all — comprises what is known as the quantum measurement problem. 

As a testament to its confounding qualities, there exists a long menu of interpretations of quantum mechanics. The most popular is the Copenhagen interpretation, which asserts that particles do not have definite properties until they are observed and the wavefunction undergoes a collapse. This is the quantum mechanics all undergraduate physics majors are introduced to, yet plenty more interpretations exist, some with slightly different flavorings of the Copenhagen dish — containing a base of wavefunction collapse with varying toppings. A new work, by Kok-Wei Bong et al., is now providing a lens through which to discern and test Copenhagen-like interpretations, casting the quantum measurement problem in a new light. But before we dive into this rich tapestry of observation and the basic nature of reality, let’s get a feel for what we’re dealing with. 

The story starts as a historical one, with high-profile skeptics of quantum theory. In response to its advent, Einstein, Podolsky, and Rosen (EPR) proposed hidden variable theories which sought to retain the idea that reality was inherently deterministic, built on relativistic notions while probabilities could be explained away by some unseen, underlying mechanism. Bell formulated a theorem to address the EPR paper, showing that the probabilistic paradigm posed by quantum mechanics cannot be entirely described by hidden variables. 

In seeking to show that quantum mechanics is an incomplete theory, EPR focused their work on what they found to be the most objectionable phenomenon: entanglement. Since entanglement is often misrepresented, let’s provide a brief overview here. When a particle decays into two daughter particles, we can perform subsequent measurements on each of those particles. When the spin angular momentum of one particle is measured, the spin angular momentum of the other particle is simultaneously measured to be exactly the value that adds to give the total spin angular momentum of the original particle (pre-decay). In this way, knowledge about the one particle gives us knowledge about the other particle; the systems are entangled. A paradox ensues since it appears that some information must have been transmitted between the two particles instantaneously. Yet entanglement phenomena really come down to a lack of sufficient information, as we are unsure of the spin measured on one particle until it is transmitted to the measurer of the second particle. 

We can illustrate this by considering the classical analogue. Think of a ball splitting in two — each ball travels in some direction and the sum total of the individual spin angular momenta is equal to the total spin angular momenta that was initiated when they existed as a group. However, I am free to catch one of the balls, or to perform a state-altering measurement, and this does not affect the value obtained by the other ball. Once the pieces are free of each other, they can acquire angular momentum from outside influences, breaking the collective initial “total” of spin angular momentum. I am also free to track these results from a distance, and as we can physically see the balls come loose and fly off in opposite directions (a form of measurement), we have all the information we need about the system. In considering the quantum version, we are left to confront a feature of quantum measurement: measurement itself alters the system that is being measured. The classical and quantum seem to contradict one another.

Bell’s Theorem made this contradiction concrete and testable by considering two entangled qubits and predicting their correlations. He posited that, if a pair of spin-½ particles in a collective singlet state were traveling in opposite directions from each other, their spins can be independently measured at distant locations with respect to axes of choice. The probability of obtaining values corresponding to an entanglement scenario then depends on the relative angle between each particle’s axes. Over many iterations of this experiment, correlations can be constructed by taking the average of the products of measurement pairs. Comparing to the case of a hidden variable theory, with an upper-limit given by assuming an underlying deterministic reality, results in inequalities that hold should these hidden variable theories be viable. Experiments designed to test the assumptions of quantum mechanics have thus far all resulted in violations of Bell-type inequalities, leaving quantum theory on firm footing. 

Now, the Kok-Wei Bong et al. research is building upon these foundations. Via consideration of Wigner’s friend paradox, the team formulated a new no-go theorem (a type of theorem that asserts a particular situation to be physically impossible) that reconsiders our ideas of what reality means and which axioms we can use to model it. Bell’s Theorem, although seeking to test our baseline assumptions of the quantum world, still necessarily rests upon a few axioms. This new theorem shows that one of a few assumptions (deemed the Local Friendliness assumptions), which had previously seemed entirely reasonable, must be incorrect in order to be compatible with quantum theory:

1. Absoluteness of observed events: Every event exists absolutely, not relatively. While the event’s details may be observer-dependent, the existence of the event is not.
2. Locality: Local settings cannot influence distant outcomes (no superluminal communication).
3. No-superdeterminism: We can freely choose the settings in our experiment and, before making this choice, our variables will not be correlated with those settings.

The work relies on the presumptive ability of a superobserver, a special kind of observer that is able to manipulate the states controlled by a friend, another observer. In the context of the “friend” being cast as an artificial intelligence algorithm in a large quantum computer, with the programmer as the superobserver, this scenario becomes slightly less fantastical. Essentially, this thought experiment digs into our ideas of the scale of applicability of quantum mechanics — what an observer is, and if quantum theory similarly applies to all observers.

To illustrate this more precisely, and consider where we might hit some snags in this analysis, let’s look at a quantum superposition state,

.

If we were to take everything we learned in university quantum mechanics courses at face value, we could easily recognize that, upon measurement, this state can be found in either the or state with equal probability. However, let us now turn our attention toward the Wigner’s friend scenario: image that Wigner has a friend inside a laboratory performing an experiment and Wigner himself is outside of the laboratory, positioned ideally as a superobserver (he can freely perform any and all quantum experiments on the laboratory from his vantage point). Going back to the superposition state above, it remains true that Wigner’s friend can observe either up or down states with 50% probability upon measurement. However, we also know that states must evolve unitarily. Wigner, still positioned outside of the laboratory, continues to observe a superposition of states with ill-defined measurement outcomes. Hence, a paradox, and one formed due to the fundamental assumption that quantum mechanics applies at all scales to all observers. This is the heart of the quantum measurement problem.

Now, let’s extend this scenario, taking our usual friends Alice and Bob as superobservers to two separate laboratories. Charlie, in the laboratory observed by Alice, has a system of spin-½ particles with an associated Hilbert space, while Debbie, in the laboratory observed by Bob, has her own system of spin-½ particles with an associated Hilbert space. Within their separate laboratories, they make measurements of the spins of the particles along the z-axis and record their results. Then Alice and Bob, still situated outside the laboratories of their respective friends, can make three different types of measurements on the systems, one of which they choose to perform randomly. First, Alice could look inside Charlie’s laboratory, view his measurement, and assign it to her own. Second, Alice could restore the laboratory to some previous state. Third, Alice could erase Charlie’s record of results and instead perform her own random measurement directly on the particle. Bob can perform the same measurements using Debbie’s laboratory.

With this setup, the new theorem then identifies a set of inequalities derived from Local Friendliness correlations, which are extended from those given by Bell’s Theorem and can be independently violated. The authors then concocted a proof-of-principle experiment, which relies on explicitly thinking of the friends Charlie and Debbie as qubits, rather than people. Using the three measurement settings and choosing systems of polarization-encoded photons, the photon paths are then the “friends” (the photon either takes Charlie’s path, Debbie’s path, or some superposition of the two). After running this experiment some thousands of times, the authors concluded that their Local Friendliness inequalities should be violated, implying that one of the three initial assumptions cannot be correct. 

The primary difference between this work and Bell’s Theorem is that it contains no prior assumptions about the underlying determinism of reality, including any hidden variables that could be used to predetermine the outcomes of events. The theorem itself is therefore built upon assumptions strictly weaker than those of Bell’s inequalities, meaning that any violations would lead to strictly stronger conclusions. This paves a promising pathway for future questions and experiments about the nature of observation and measurement, narrowing down the large menu of interpretations of quantum mechanics. The question of which of the assumptions — absoluteness of observed events, locality, and no-superdeterminism — is incorrect is left as an open question. While the first two are widely used throughout physics, the assumption of no-superdeterminism digs down into the question of what measurement really means and what is classed as an observer. These points will doubtlessly be in contention as physicists continue to explore the oddities that quantum theory has to offer, but this new theorem offers promising results on the path to understanding the quirky quantum world.

Further Reading:

1. More details on Bell’s Theorem: https://arxiv.org/pdf/quant-ph/0402001.pdf 
2. Frank Wilczek’s column on entanglement: https://www.quantamagazine.org/entanglement-made-simple-20160428/ 
3. Philosophical issues in quantum theory: https://plato.stanford.edu/entries/qt-issues/ 

Particle physics, like its overarching fields of physics and astronomy, has a diversity problem. Black students and researchers are severely underrepresented in our field, and many of them report feeling unsupported, unincluded, and undervalued throughout their careers. Although Black students enter into the field as undergraduates at comparable rates to white students, 8.5 times more white students than Black students enter PhD programs in physics¹. This suggests that the problem lies not in generating interest for the subject, but in the creation of an inclusive space for science.

This isn’t new information, although it has arguably not received the full attention it deserves, perhaps because everybody has not been on the same page. Before we go any further, let’s start with the big question: why is diversity in physics important? In an era where physics research is done increasingly collaboratively, the processes of cultivating talent across the social and racial spectrum is a strength that benefits all physicists. Having team members who can ask new questions or think differently about a problem leads to a wider variety of ideas and creativity in problem-solving approaches. It is advantageous to diversify a team, as the cohesiveness of the team often matters more in collaborative efforts than the talents of the individual members. While bringing on individuals from different backgrounds doesn’t guarantee the success of this endeavor, it does increase the probability of being able to tackle a problem using a variety of approaches. This is critical to doing good physics.

This naturally leads us to an analysis of the current state of diversity in physics. We need to recognize that physics is both subject to the underlying societal current of white supremacy and often perpetuates it through unconscious biases that manifest in bureaucratic structures, admissions and hiring policies, and harmful modes of unchecked communication. This is a roadblock to the accessibility of the field to the detriment of all physicists, as high attrition rates for a specific group suggests a loss of talent. But more than that, we should be striving to create departments and workplaces where all individuals and their ideas are values and welcomed. In order to work toward this, we need to: 

1. Gather data: Why are Black students and researchers leaving the field at significantly higher rates? What is it like to be Black in physics?
2. Introspect: What are we doing (or not doing) to support Black students in physics classrooms and departments? How have I contributed to this problem? How has my department contributed to this problem? How can I change these behaviors and advocate for others?
3. Act: Often, well-meaning discussions remain just that — discussions. How can we create accountability to ensure that any agreed-upon action items are carried out? How can we track this progress over time?

Luckily, on the first point, there has been plenty of data that has already been gathered, although further studies are necessary to widen the scope of our understanding. Let’s look at the numbers. 

Black representation at the undergraduate level is the lowest in physics out of all the STEM fields, at roughly 3%. This number has decreased from 5% in 1999, despite the total number of bachelor’s degrees earned in physics more than doubling during that time² (note: 13% of the United States population is Black). While the number of bachelor’s degrees earned by Black students increased by 36% across the physical sciences from 1995 to 2015, the corresponding percentage solely for physics degrees increased by only 4%². This suggests that, while access has theoretically increased, retention has not. This tells a story of extra barriers for Black physics students that push them away from the field.

This is corroborated as we move up the academic ladder. At the graduate level, the total number of physics PhDs awarded to Black students has fluctuated between 10 and 20 from 1997 to 2012⁴. From 2010 to 2012, only 2% of physics doctoral students in the United States were Black out of a total of 843 total physics PhDs⁴. For Black women, the numbers are the most dire, having received only 22 PhDs in astronomy and 144 PhDs in physics or closely-related fields in the entire history of United States physics graduate programs. Meanwhile, the percentage of Black faculty members from 2004 to 2012 has stayed relatively consistent, hovering around 2%⁵. Black students and faculty alike often report being the sole Black person in their department. 

Where do these discrepancies come from? In January, the American Institute for Physics (AIP) released its TEAM-UP report summarizing what it found to be the main causes for Black underrepresentation in physics. According to the report, a main contribution to these numbers is whether students are immersed in a supportive environment². With this in mind, the above statistics are bolstered by anecdotal evidence and trends. Black students are less likely to report a sense of belonging in physics and more likely to report experiencing feelings of discouragement due to interactions with peers². They report lower levels of confidence and are less likely to view themselves as scientists². When it comes to faculty interaction, they are less likely to feel comfortable approaching professors and report fewer cases of feeling affirmed by faculty². Successful Black faculty describe gatekeeping in hiring processes, whereby groups of predominantly white male physicists are subject to implicit biases and are more likely to accept students or hire faculty who remind them of themselves³. 

It is worth noting that this data comes in light of the fact that diversity programs have been continually implemented during the time period of the study. Most of these programs focus on raising awareness of a diversity problem, scraping at the surface instead of digging deeper into the foundations of this issue. Clearly, this approach has fallen short, and we must shift our efforts. The majority of diversity initiatives focus on outlawing certain behaviors, which studies suggest tends to reaffirm biased viewpoints and lead to a decrease in overall diversity⁶. These programs are often viewed as a solution in their own right, although it is clear that simply informing a community that bias exists will not eradicate it. Instead, a more comprehensive approach, geared toward social accountability and increased spaces for voluntary learning and discussion, might garner better results. 

On June 10th, a team of leading particle physicists around the world published an open letter calling for a strike, for Black physicists to take a much-needed break from emotional heavy-lifting and non-Black physicists to dive into the self-reflection and conversation that is necessary for such a shift. The authors of the letter stressed, “Importantly, we are not calling for more diversity and inclusion talks and seminars. We are not asking people to sit through another training about implicit bias. We are calling for every member of the community to commit to taking actions that will change the material circumstances of how Black lives are lived — to work toward ending the white supremacy that not only snuffs out Black physicist dreams but destroys whole Black lives.” 

“…We are calling for every member of the community to commit to taking actions that will change the material circumstances of how Black lives are lived — to work toward ending the white supremacy that not only snuffs out Black physicist dreams but destroys whole Black lives.” -Strike for Black Lives

Black academics, including many physicists, took to Twitter to detail their experiences under the hashtag #Blackintheivory. These stories painted a poignant picture of discrimination: being told that an acceptance to a prestigious program was only because “there were no Black women in physics,” being required to show ID before entering the physics building on campus, being told to “keep your head down” in response to complaints of discrimination, and getting incredulous looks from professors in response to requests for letters of recommendation. Microaggressions — brief and commonplace derisions, derogatory terms, or insults toward a group of people — such as these are often described as being poked repeatedly. At first, it’s annoying but tolerable, but over time it becomes increasingly unbearable. We are forcing Black students and faculty to constantly explain themselves, justify their presence, and prove themselves far more than any other group. While we all deal with the physics problem sets, experiments, and papers that are immediately in front of us, we need to recognize the further pressures that exist for Black students and faculty. It is much more difficult to focus on a physics problem when your society or department questions your right to be where you are. In the hierarchy of needs, it’s obvious which comes first. 

Physicists, I’ve observed, are especially proud of the field they study. And rightfully so — we tackle some of the deepest, most fundamental questions the universe has to offer. Yet this can breed a culture of arrogance and “lone genius” stereotypes, with brilliant idolized individuals often being white older males. In an age of physics that is increasingly reliant upon large collaborations such as CERN and LIGO, this is not only inaccurate but actively harmful. The vast majority of research is done in teams, and creating a space where team members can feel comfortable is paramount to its success. Often, we can put on a show of being bastions of intellectual superiority, which only pushes away students who are not as confident in their abilities or who look around the room and see nobody else like them in it.

Further, some academics use this proclaimed superiority to argue their way around any issues of diversity and inclusion, choosing to see the data (such as GPA or test scores) without considering the context. Physicists tend to tackle problems in an inherently academic, systematic fashion. We often remove ourselves from consideration because we want physics to stick to a scientific method free from bias on behalf of the experimenter. Yet physics, as a human activity undertaken by groups of individuals from a society, cannot be fully separated from the society in which it is practiced. We need to consider: Who determines allocation of funding? Who determines which students are admitted, or which faculty are hired? 

In order to fully transform the systems that leave Black students and faculty in physics underrepresented, unsupported, and even blatantly pushed out of the field, we must do the internal work as individuals and as departments to recognize harmful actions and put new systems in place to overturn these policies. With that in mind, what is the way forward? While there may be an increase in current momentum for action on this issue, it is critical to find a sustainable solution. This requires having difficult conversations and building accountability in the long term by creating or joining a working group within a department focused on equity, diversity, and inclusion (EDI) efforts. These types of fundamental changes are not possible without more widespread involvement; often, the burden of changing the system often falls on members of minority groups. The TEAM-UP report published several recommendations, centered on several categories including the creation of a resource guide, re-evaluating harassment response, and collecting data in an ongoing fashion. Further, Black scientists have long urged for the following actions⁷:

1. The creation of opportunities for discussion amongst colleagues on these issues. This could be accomplished through working groups or reading groups within departments. The key is having a space solely focused on learning more deeply about EDI.
2. Commitments to bold hiring practices, including cluster hiring. This occurs when multiple Black faculty members are hired at once, in order to decrease the isolation that occurs from being the sole Black member of a department. 
3. The creation of a welcoming environment. This one is trickier, given that the phrase “welcoming environment” means something different to different people. An easier way to get a feel for this is by collecting data within a department, of both satisfaction and any personal stories or comments students or faculty would like to report. This also requires an examination of microaggressions and general attitudes toward Black members of a department, as an invite to the table could also be a case of tokenization. 
4. A commitment to transparency. Research has shown that needing to explain hiring decisions to a group leads to a decrease in bias⁶. 

While this is by no means a comprehensive list, there are concrete places for all of us to start. 

References:

1. https://physicstoday.scitation.org/doi/10.1063/PT.3.3536
2. https://www.aip.org/sites/default/files/aipcorp/files/teamup-full-report.pdf
3. https://www.insidehighered.com/advice/2018/03/09/mentors-and-role-models-can-attract-minority-students-fields-where-they-may-not
4. https://www.aps.org/careers/statistics/upload/trends-phd0214.pdf
5. https://www.aip.org/sites/default/files/statistics/faculty/africanhisp-fac-pa-12.pdf
6. https://hbr.org/2016/07/why-diversity-programs-fail 
7. https://www.nature.com/articles/d41586-020-01883-8

Title: “Upper Bound of Neutrino Masses from Combined Cosmological Observations and Particle Physics Experiments”

Author: Loureiro et al. 

Reference: https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.123.081301

Neutrinos are almost a lot of things. They are almost massless, a property that goes against the predictions of the Standard Model. Possessing this non-zero mass, they should travel at almost the speed of light, but not quite, in order to be consistent with the principles of special relativity. Yet each measurement of neutrino propagation speed returns a value that is, within experimental error, exactly the speed of light. Only coupled to the weak force, they are almost non-interacting, with 65 billion of them streaming from the sun through each square centimeter of Earth each second, almost undetected. 

How do all of these pieces fit together? The story of the neutrino begins in 1930, when Wolfgang Pauli propositioned an as-yet detected particle emitted during beta decay in order to explain an observed lack of energy and momentum conservation. In 1956, an antineutrino-positron annihilation producing two gamma rays was detected, confirming the existence of neutrinos. Yet with this confirmation came an assortment of growing mysteries. In the decades that followed, a series of experiments found that there are three distinct flavors of neutrino, one corresponding to each type of lepton: electron, muon, and tau particles. Subsequent measurements of propagating neutrinos then revealed a curious fact: these three flavors are anything but distinct. When the flavor of a neutrino is initially measured to be, say, an electron neutrino, a second measurement of flavor after it has traveled some distance could return the answer of muon neutrino. Measure yet again, and you could find yourself a tau neutrino. This process, in which the probability of measuring a neutrino in one of the three flavor states varies as it propagates, is known as neutrino oscillation. 

Neutrino oscillation threw a wrench into the Standard Model in terms of mass; neutrino oscillation implies that the masses of the three neutrino flavors cannot be equal to each other, and hence cannot all be zero. Specifically, only one of them would be allowed to be zero, with the remaining two non-zero and non-equal. While at first glance an oddity, oscillation arises naturally from underlying mathematics, and we can arrive at this conclusion via a simple analysis. To think about a neutrino, we consider two eigenstates (the state a particle is in when it is measured to have a certain observable quantity), one corresponding to flavor and one corresponding to mass. Because neutrinos are created in weak interactions which conserve flavor, they are initially in a flavor eigenstate. Flavor and mass eigenstates cannot be simultaneously determined, and so each flavor eigenstate is a linear combination of mass eigenstates, and vice versa. Now, consider the case of three flavors of neutrino. If all three flavors consisted of the same linear combination of mass eigenstates, there would be no varying superposition between them, since the different masses would travel at different speeds in accordance with special relativity. Since we experimentally observe an oscillation between neutrino flavors, we can conclude that their masses cannot all be the same.

Although this result was unexpected and provides the first known departure from the Standard Model, it is worth noting that it also neatly resolves a few outstanding experimental mysteries, such as the solar neutrino problem. Neutrinos in the sun are produced as electron neutrinos and are likely to interact with unbound electrons as they travel outward, transitioning them into a second mass state which can interact as any of the three flavors. By observing a solar neutrino flux roughly a third of its predicted value, physicists not only provided a potential answer to a previously unexplained phenomenon but also deduced that this second mass state must be larger than the state initially produced. Related flux measurements of neutrinos produced during charged particle interactions in the Earth’s upper atmosphere, which are primarily muon neutrinos, reveal that the third mass state is quite different from the first two mass states. This gives rise to two potential mass hierarchies: the normal () and inverted () ordering.

However, this oscillation also means that it is difficult to discuss neutrino masses individually, as measuring the sum of neutrino masses is currently easier from a technical standpoint. With current precision in cosmology, we cannot distinguish the three neutrinos at the epoch in which they become free-traveling, although this could change with increased precision. Future experiments in beta decay could also lead to progress in pinpointing individual masses, although current oscillation experiments are only sensitive to mass-squared differences . Hence, we frame our models in terms of these mass splittings and the mass sum, which also makes it easier to incorporate cosmological data. Current models of neutrinos are phenomenological ― not directly derived from theory but consistent with both theoretical principles and experimental data. The mixing between states is mathematically described by the PMNS (Pontecorvo-Maki-Nakagawa-Sakata) matrix, which is parametrized by three mixing angles and a phase related to CP violation. These parameters, as in most phenomenological models, have to be inserted into the theory. There is usually a wide space of parameters in such models and constraining this space requires input from a variety of sources. In the case of neutrinos, both particle physics experiments and cosmological data provide key avenues for exploration into these parameters. In a recent paper, Loureiro et al. used such a strategy, incorporating data from the large scale structure of galaxies and the cosmic microwave background to provide new upper bounds on the sum of neutrino masses.

The group investigated two main classes of neutrino mass models: exact models and cosmological approximations. The former concerns models that integrate results from neutrino oscillation experiments and are parametrized by the smallest neutrino mass, while the latter class uses a model scheme in which the neutrino mass sum is related to an effective number of neutrino species times an effective mass which is equal for each flavor. In exact models, Gaussian priors (an initial best-guess) were used with data sampling from a number of experimental results and error bars, depending on the specifics of the model in question. This includes possibilities such as fixing the mass splittings to their central values or assuming either a normal or inverted mass hierarchy. In cosmological approximations, was fixed to a specific value depending on the particular cosmological model being studied, with the total mass sum sampled from data.

The group ultimately demonstrated that cosmologically-based models result in upper bounds for the mass sum that are much lower than those generated from physically-motivated exact models, as we can see in the figure above. One of the models studied resulted in an upper bound that is not only different from those determined from neutrino oscillation experiments, but is inconsistent with known lower bounds. This puts us into the exciting territory that neutrinos have pushed us to again and again: a potential finding that goes against what we presently know. The calculated upper bound is also significantly different if the assumption is made that one of the neutrino masses is zero, with the mass sum contained in the remaining two neutrinos, setting the stage for future differentiation between neutrino masses. Although the group did not find any statistically preferable model, they provide a framework for studying neutrinos with a considerable amount of cosmological data, using results of the Planck, BOSS, and SDSS collaborations, among many others. Ultimately, the only way to arrive at a robust answer to the question of neutrino mass is to consider all of these possible sources of information for verification. 

With increased sensitivity in upcoming telescopes and a plethora of intriguing beta decay experiments on the horizon, we should be moving away from studies that update bounds and toward ones which make direct estimations. In these future experiments, previous analysis will prove vital in working toward an understanding of the underlying mass models and put us one step closer to unraveling the enigma of the neutrino. While there are still many open questions concerning their properties ― Why are their masses so small? Is the neutrino its own antiparticle? What governs the mass mechanism? ― studies like these help to grow intuition and prepare for the next phases of discovery. I’m excited to see what unexpected results come next for this almost elusive particle.

Further Reading:

1. A thorough introduction to neutrino oscillation: https://arxiv.org/pdf/1802.05781.pdf
2. Details on mass ordering: https://arxiv.org/pdf/1806.11051.pdf
3. More information about solar neutrinos (from a fellow ParticleBites writer!): https://particlebites.com/?p=6778 
4. A summary of current neutrino experiments and their expected results: https://www.symmetrymagazine.org/article/game-changing-neutrino-experiments 

Title: “Searching for dark photon dark matter in LIGO O1 data”

Author: Huai-Ke Guo, Keith Riles, Feng-Wei Yang, & Yue Zhao

Reference: https://www.nature.com/articles/s42005-019-0255-0

There is very little we know about dark matter save for its existence. Its mass(es), its interactions, even the proposition that it consists of particles at all is mostly up to the creativity of the theorist. For those who don’t turn to modified theories of gravity to explain the gravitational effects on galaxy rotation and clustering that suggest a massive concentration of unseen matter in the universe (among other compelling evidence), there are a few more widely accepted explanations for what dark matter might be. These include weakly-interacting massive particles (WIMPS), primordial black holes, or new particles altogether, such as axions or dark photons. 

In particle physics, this latter category is what’s known as the “hidden sector,” a hypothetical collection of quantum fields and their corresponding particles that are utilized in theorists’ toolboxes to help explain phenomena such as dark matter. In order to test the validity of the hidden sector, several experimental techniques have been concocted to narrow down the vast parameter space of possibilities, which generally consist of three strategies:

1. Direct detection: Detector experiments look for low-energy recoils of dark matter particle collisions with nuclei, often involving emitted light or phonons. 
2. Indirect detection: These searches focus on potential decay products of dark matter particles, which depends on the theory in question.
3. Collider production: As the name implies, colliders seek to produce dark matter in order to study its properties. This is reliant on the other two methods for verification.

The first detection of gravitational waves from a black hole merger in 2015 ushered in a new era of physics, in which the cosmological range of theory-testing is no longer limited to the electromagnetic spectrum. Bringing LIGO (the Laser Interferometer Gravitational-Wave Observatory) to the table, proposals for the indirect detection of dark matter via gravitational waves began to spring up in the literature, with implications for primordial black hole detection or dark matter ensconced in neutron stars. Yet a new proposal, in a paper by Guo et. al., suggests that direct dark matter detection with gravitational waves may be possible, specifically in the case of dark photons. 

Dark photons are hidden sector particles in the ultralight regime of dark matter candidates. Theorized as the gauge boson of a U(1) gauge group, meaning the particle is a force-carrier akin to the photon of quantum electrodynamics, dark photons either do not couple or very weakly couple to Standard Model particles in various formulations. Unlike a regular photon, dark photons can acquire a mass via the Higgs mechanism. Since dark photons need to be non-relativistic in order to meet cosmological dark matter constraints, we can model them as a coherently oscillating background field: a plane wave with amplitude determined by dark matter energy density and oscillation frequency determined by mass. In the case that dark photons weakly interact with ordinary matter, this means an oscillating force is imparted. This sets LIGO up as a means of direct detection due to the mirror displacement dark photons could induce in LIGO detectors.

LIGO consists of a Michelson interferometer, in which a laser shines upon a beam splitter which in turn creates two perpendicular beams. The light from each beam then hits a mirror, is reflected back, and the two beams combine, producing an interference pattern. In the actual LIGO detectors, the beams are reflected back some 280 times (down a 4 km arm length) and are split to be initially out of phase so that the photodiode detector should not detect any light in the absence of a gravitational wave. A key feature of gravitational waves is their polarization, which stretches spacetime in one direction and compresses it in the perpendicular direction in an alternating fashion. This means that when a gravitational wave passes through the detector, the effective length of one of the interferometer arms is reduced while the other is increased, and the photodiode will detect an interference pattern as a result. 

LIGO has been able to reach an incredible sensitivity of one part in in its detectors over a 100 Hz bandwidth, meaning that its instruments can detect mirror displacements up to 1/10,000th the size of a proton. Taking advantage of this number, Guo et. al. demonstrated that the differential strain (the ratio of the relative displacement of the mirrors to the interferometer’s arm length, or ) is also sensitive to ultralight dark matter via the modeling process described above. The acceleration induced by the dark photon dark matter on the LIGO mirrors is ultimately proportional to the dark electric field and charge-to-mass ratio of the mirrors themselves.

Once this signal is approximated, next comes the task of estimating the background. Since the coherence length is of order m for a dark photon field oscillating at order 100 Hz, a distance much larger than the separation between the LIGO detectors at Hanford and Livingston (in Washington and Louisiana, respectively), the signals from dark photons at both detectors should be highly correlated. This has the effect of reducing the noise in the overall signal, since the noise in each of the detectors should be statistically independent. The signal-to-noise ratio can then be computed directly using discrete Fourier transforms from segments of data along the total observation time. However, this process of breaking up the data, known as “binning,” means that some signal power is lost and must be corrected for.

In applying this analysis to the strain data from the first run of Advanced LIGO, Guo et. al. generated a plot which sets new limits for the coupling of dark photons to baryons as a function of the dark photon oscillation frequency. There are a few key subtleties in this analysis, primarily that there are many potential dark photon models which rely on different gauge groups, yet this framework allows for similar analysis of other dark photon models. With plans for future iterations of gravitational wave detectors, further improved sensitivities, and many more data runs, there seems to be great potential to apply LIGO to direct dark matter detection. It’s exciting to see these instruments in action for discoveries that were not in mind when LIGO was first designed, and I’m looking forward to seeing what we can come up with next!

Learn More:

1. An overview of gravitational waves and dark matter: https://www.symmetrymagazine.org/article/what-gravitational-waves-can-say-about-dark-matter
2. A summary of dark photon experiments and results: https://physics.aps.org/articles/v7/115 
3. Details on the hardware of Advanced LIGO: https://arxiv.org/pdf/1411.4547.pdf
4. A similar analysis done by Pierce et. al.: https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.121.061102

Title: “New physics implications of recent search for at KOTO”

Author: Kitahara et. al.

Reference: https://arxiv.org/pdf/1909.11111.pdf

The Standard Model, though remarkably accurate in its depiction of many physical processes, is incomplete. There are a few key reasons to think this: most prominently, it fails to account for gravitation, dark matter, and dark energy. There are also a host of more nuanced issues: it is plagued by “fine tuning” problems, whereby its parameters must be tweaked in order to align with observation, and “free parameter” problems, which come about since the model requires the direct insertion of parameters such as masses and charges rather than providing explanations for their values. This strongly points to the existence of as-yet undetected particles and the inevitability of a higher-energy theory. Since gravity should be a theory living at the Planck scale, at which both quantum mechanics and general relativity become relevant, this is to be expected. 

A promising strategy for probing physics beyond the Standard Model is to look at decay processes that are incredibly rare in nature, since their small theoretical uncertainties mean that only a few event detections are needed to signal new physics. A primary example of this scenario in action is the discovery of the positron via particle showers in a cloud chamber back in 1932. Since particle physics models of the time predicted zero anti-electron events during these showers, just one observation was enough to herald a new particle. 

The KOTO experiment, conducted at the Japan Proton Accelerator Research Complex (J-PARC), takes advantage of this strategy. The experiment was designed specifically to investigate a promising rare decay channel: , the decay of a neutral long kaon into a neutral pion, a neutrino, and an antineutrino. Let’s break down this interaction and discuss its significance. The kaon, a meson composed of an up quark and anti-strange quark, comes in both long and short varieties, describing the time of decay relative to each other. The Standard Model predicts a branching ratio of for this particular decay process, meaning that out of all the neutral long kaons that decay, only this tiny fraction of them decay into the combination of a neutral pion, neutrino, and an antineutrino, making it incredibly rare for this process to be observed in nature.

Here’s where it gets exciting. The KOTO experiment recently reported four signal events within this decay channel where the Standard Model predicts just events. If all four of these events are confirmed as the desired neutral long kaon decays, new physics is required to explain the enhanced signal. There are several possibilities, recently explored in a new paper by Kitahara et. al.,  for what this new physics might be. Before we go into too much detail, let’s consider how KOTO’s observation came to be.

The KOTO experiment is a fixed-target experiment, in which particles are accelerated and collide with something stationary. In this case, protons at energy 30 GeV collided with gold, producing a beam of kaons after other products are diverted with collimators and magnets. The observation of the desired mode is particularly difficult experimentally for several reasons. First, the initial and final decay products are neutrally charged, making them harder to detect since they do not ionize, a primary strategy for detecting charged particles. Second, neutral pions are produced via several other kaon decay channels, requiring several strategies to differentiate neutral pions produced by from those produced from , , and , among others. As we can see in the Feynman diagram above, our desired decay mode has the advantage of producing two photons, allowing KOTO to observe these photons and their transverse momentum in order to pinpoint a  decay. In terms of experimental construction, KOTO included charged veto detectors in order to reject events with charged particles in the final state and a systematic study of background events was performed in order to discount hadron showers originating from neutrons in the beam line. 

This setup was in service of KOTO’s goal to explore the question of CP violation with long kaon decay. CP violation refers to the violation of charge-parity symmetry, the combination of charge-conjugation symmetry (in which a theory is unchanged when we swap a particle for its antiparticle) and parity symmetry (in which a theory is invariant when left and right directions are swapped). We seek to understand why some processes seem to preserve CP symmetry when the Standard Model allows for violation, as is the case in quantum chromodynamics (QCD), and why some processes break CP symmetry, as is seen in the quark mixing matrix (CKM matrix) and the neutrino oscillation matrix. Overall, CP violation has implications for matter-antimatter asymmetry, the question of why the universe seems to be composed predominantly of matter when particle creation and decay processes produce equal amounts of both matter and antimatter. An imbalance of matter and antimatter in the universe could be created if CP violation existed under the extreme conditions of the early universe, mere seconds after the Big Bang. Explanations for matter-antimatter asymmetry that do not involve CP violation generally require the existence of primordial matter-antimatter asymmetry, effectively dodging the fundamental question. The observation of CP violation with KOTO could provide critical evidence toward an eventual answer.  

The Kitahara paper provides three interpretations of KOTO’s observation that incorporate physics beyond the Standard Model: new heavy physics, new light physics, and new particle production. The first, new heavy physics, amplifies the expected Standard Model signal via the incorporation of new operators that couple to existing Standard Model particles. If this coupling is suppressed, it could adequately explain the observed boost in the branching ratio. Light new physics involves reinterpreting the neutrino-antineutrino pair as a new light particle. Factoring in experimental constraints, this new light particle should decay in with a finite lifetime on the order of 0.1-0.01 nanoseconds, making it almost completely invisible to experiment. Finally, new particles could be produced within the decay channel, which should be light and long-lived in order to allow for its decay to two photons. The details of these new particle scenarios should involve constraints from other particle physics processes, but each serve to increase the branching ratio through direct production of more final state particles. On the whole, this demonstrates the potential for the to provide a window to physics beyond the Standard Model. 

Of course, this analysis presumes the accuracy of KOTO’s four signal events. Pending the confirmation of these detections, there are several exciting possibilities for physics beyond the Standard Model, so be sure to keep your eye on this experiment!

Learn More:

1. An overview of the KOTO experiment’s data taking: https://arxiv.org/pdf/1910.07585.pdf
2. A description of the sensitivity involved in the KOTO experiment’s search: https://j-parc.jp/en/topics/2019/press190304.html
3. More insights into CP violation: https://www.symmetrymagazine.org/article/charge-parity-violation

Title: “Probing dense baryon-rich matter with virtual photons”

Author: HADES Collaboration

Reference: https://www.nature.com/articles/s41567-019-0583-8

The quark-gluon plasma, a sea of unbound quarks and gluons moving at relativistic speeds thought to exist at extraordinarily high temperature and density, is a phase of matter critical to our understanding of the early universe and extreme stellar interiors. On the timescale of milliseconds after the Big Bang, the matter in the universe is postulated to have been in a quark-gluon plasma phase, before the universe expanded, cooled, and formed the hadrons we observe today from constituent quarks and gluons. The study of quark matter, the range of phases formed from quarks and gluons, can provide us with insight into the evanescent early universe, providing an intriguing focus for experimentation. Astrophysical objects that are comprised of quarks, such as neutron stars, are also thought to house the necessary conditions for the formation of quark-gluon plasma at their cores. With the accumulation of new data from neutron star mergers, studies of quark matter are becoming increasingly productive and rife for new discovery. 

Quantum chromodynamics (QCD) is the theory of quarks and the strong interaction between them. In this theory, quarks and force-carrying gluons, the aptly-named particles that “glue” quarks together, have a “color” charge analogous to charge in quantum electrodynamics (QED). In QCD, the gluon field is often modeled as a narrow tube between two color charges with a constant strong force between them, in contrast with the inverse-square dependence on distance for fields in QED. The pair potential energy between the quarks increases linearly with separation, eventually surpassing the creation energy for a new quark-antiquark pair. Hence, the quarks cannot exist in unbound pairs at low energies, a property known as color confinement. When separation is attempted between quarks, new quarks are instead produced. In particle accelerators, physicists see “jets” of new color-neutral particles (mesons and baryons) in the process of hadronization. At high energies, the story changes and hinges on an idea known as asymptotic freedom, in which the strength of particle interactions decreases with increased energy scale in certain gauge theories such as QCD. 

QCD matter is commonly probed with heavy-ion collision experiments and quark-gluon plasma has been produced before in minute quantities at the Relativistic Heavy Ion Collider (RHIC) at Brookhaven National Lab as well as the Large Hadron Collider (LHC) at CERN. The goal of these experiments is to create conditions similar to those of the early universe or at the center of dense stars — doing so requires intense temperatures and an abundance of quarks. Heavy-ions, such as gold or lead nuclei, fit this bill when smashed together at relativistic speeds. When these collisions occur, the resulting “fireball” of quarks and gluons is unstable and quickly decays into a barrage of new, stable hadrons via the hadronization method discussed above. 

There are several main goals of heavy-ion collision experiments around the world, revolving around the study of the phase diagram for quark matter. The first component of this is the search for the critical point: the endpoint of the line of first-order phase transitions. The phase transition between hadronic matter, in which quarks and gluons are confined, and partonic matter, in which they are dissociated in a quark-gluon plasma, is also an active area of investigation. There is additionally an ongoing search for chiral symmetry restoration at finite temperature and finite density. A chiral symmetry occurs when the handedness of the particles remains invariant under a parity transformation, that is, when the sign of a spatial coordinate is flipped. However, in QCD, a symmetric system becomes asymmetric in a process known as spontaneous symmetry breaking. Several experiments are designed to investigate evidence of the restoration of this symmetry.

The HADES (High-Acceptance DiElectron Spectrometer) collaboration is a group attempting to address such questions. In a recent experiment, HADES focused on the creation of quark matter via collisions of a beam of Au (gold) ions with a stack of Au foils. Dileptons, which are bound lepton-antilepton pairs that emerge from the decay of virtual particles, are a key element of HADES’ findings. In quantum field theory (QFT), in which particles are modeled as excitations in an underlying field, virtual particles can be thought of as excitations in the field that are transient due to limitations set by the uncertainty principle. Virtual particles are represented by internal lines in Feynman diagrams, are used as tools in calculations, and are not isolated or measured on their own — they are only exchanged with ordinary particles. In the HADES experiment, the virtual photons that produce dileptons which immediately decouple from the strong force. Produced at all stages of QCD interaction, they are ideal messengers of any modification of hadron properties. They are also thought to contain information about the thermal properties of the underlying medium. 

To actually extract this information, the HADES detector utilizes a time-of-flight chamber and ring-imaging Cherenkov (RICH) chamber, which identifies particles using the characteristics of Cherenkov radiation: electromagnetic radiation emitted when a particle travels through a dielectric medium at a velocity greater than the phase velocity of light in that particular medium. The detector is then able to measure the invariant mass, rapidity (a commonly-used substitute measure for relativistic velocity), and transverse momentum of emitted electron-positron pairs, the dilepton of choice. In accelerator experiments, there are typically a number of selection criteria in place to ensure that the machinery is detecting the desired particles and the corresponding data is recorded. When a collision event occurs within HADES, a number of checks are in place to ensure that only electron-positron events are kept, factoring in both the number of detected events and detector inefficiency, while excess and background data is thrown out. The end point of this data collection is a calculation of the four-momenta of each lepton pair, a description of its relativistic energy and momentum components. This allows for the construction of a dilepton spectrum: the distribution of the invariant masses of detected dileptons. 

The main data takeaway from this experiment was the observation of an excess of dilepton events in an exponential shape, contrasting with the expected number of dileptons from ordinary particle collisions. This suggests a shift in the properties of the underlying matter, with a reconstructed temperature above 70 MeV (note that particle physicists tend to quote temperatures in more convenient units of electron volts). The kicker comes when the group compares these results to simulated neutron star mergers, with expected core temperatures of 75 MeV. This means that the bulk matter created within HADES is similar to the highly dense matter formed in such mergers, a comparison which has become recently accessible due to multi-messenger signals incorporating both electromagnetic and gravitational wave data. 

Practically, we see that HADES’ approach is quite promising for future studies of matter under extreme conditions, with the potential to reveal much about the state of the universe early on in its history as well as probe certain astrophysical objects — an exciting realization! 

Learn More:

1. https://home.cern/science/physics/heavy-ions-and-quark-gluon-plasma
2. https://www-hades.gsi.de/
3. https://profmattstrassler.com/articles-and-posts/particle-physics-basics/virtual-particles-what-are-they/