Authors: Davide Gerosa, Christopher J. Moore
Reference: arXiv:1606.04226; Phys. Rev. Lett. 117, 011101 (2016)
On September 14 2015, something really huge happened in physics: the first direct detection of gravitational waves happened. But measuring a single gravitational wave was never the goal—.though freaking cool in and of itself of course! So what is the purpose of gravitational wave astronomy?
The idea is that gravitational waves can be used as another tool to learn more about our Universe and its components. Until the discovery of gravitational waves, observations in astrophysics and astronomy were limited to observations with telescopes and thus to electromagnetic radiation. Now a new era has started: the era of gravitational wave astronomy. And when the space-based eLISA observatory comes online, it will begin an era of gravitational wave cosmology. So what is it that we can learn from our universe from gravitational waves?
First of all, the first detection aka GW150914 was already super interesting:
- It was the first observation of a binary black hole system (with unexpected masses!).
- It put some strong constraints on the allowed deviations from Einstein’s theory of general relativity.
What is next? We hope to detect a neutron star orbiting a black hole or another neutron star. This will allow us to learn more about the equation of state of neutron stars and thus their composition. But the authors in this paper suggest another exciting prospect: observing so-called black hole kicks using gravitational wave astronomy.
So, what is a black hole kick? When two black holes rotate around each other, they emit gravitational waves. In this process, they lose energy and therefore they get closer and closer together before finally merging to form a single black hole. However, generically the radiation is not the same in all directions and thus there is also a net emission of linear momentum. By conservation of momentum, when the black holes merge, the final remnant experiences a recoil in the opposite direction. Previous numerical studies have shown that non-spinning black holes ‘only’ have kicks of ∼ 170 km per second, but you can also have “superkicks” as high as ∼5000 km per second! These speeds can exceed the escape velocity of even the most massive galaxies and may thus eject black holes from their hosts. These dramatic events have some electromagnetic signatures, but also leave an imprint in the gravitational waveform that we detect.

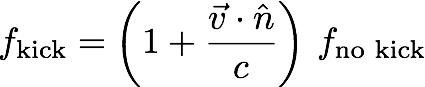
with v the kick velocity and n the unit vector in the direction from the observer to the black hole system (and c the speed of light). The black hole dynamics is entirely captured by the dimensionless number G f M/c3 with M the mass of the binary (and G Newton’s constant). So you can also model this shift in frequency by using the unkicked frequency fno kick and observing the Doppler shift into the mass. This is very convenient because this means that you can use all the current knowledge and results for the gravitational waveforms and just change the mass. Now the tricky part is that the velocity changes over time and this needs to be modelled more carefully.
A crude model would be to say that during the inspiral of the black holes (which is the long phase during which the two black holes rotate around each other – see figure 1), the emitted linear momentum is too small and the mass is unaffected by emission of linear momentum. During the final stages the black holes merge and the final remnant emits a gravitational wave with decreasing amplitude, which is called the ringdown phase. During this latter phase the velocity kick is important and one can relate the mass during inspiral Mi with the mass during the ringdown phase Mr simply by

The results of doing this for a black hole kick moving away (or towards) us are shown in fig. 2: the wave gets redshifted (or blueshifted).
![Fig. 2: If a black hole binary radiates isotropically, it does not experience any kick and the gravitational wave has the black waveform. However, if it experiences a kick along the line of sight, the waveform can get redshifted (when the system moves away from us) as shown on the left of blueshifted (when system moves toward us) as shown on the right. The top and lower panel correspond to the two independent polarizations of the gravitational wave.[Figure taken from this paper]](http://www.particlebites.com/wp-content/uploads/2016/07/figure_redshiftedwave-300x107.jpg)
Further Reading
- The websites (LIGO / eLISA) of the ground-based gravitational wave interferometer LIGO and the large scale space mission eLISA have great descriptions about their mission and the science they do: worth checking out!
- Tushna Commissariat’s article in Physics World (Feb 11, 2016): A nice (non-technical) article on the first detection of gravitational wave
- Gravitation by Misner, Thorne and Wheeler. The ‘bible’ of general relativity and gravitational waves is aka as MTW (after its authors) and is a great start for a more solid background on the basics, but does not cover black hole kicks
- arXiv:1010.5260: A review on numerical methods (including applications to kicks)
Latest posts by Beatrice Bonga (see all)
- Universality classes are not that universal (…and some of its other shortcomings) - October 5, 2016
- A new anomaly: the electromagnetic duality anomaly - September 20, 2016
- Can we measure black hole kicks using gravitational waves? - July 26, 2016
