Authors: J. Martin, C. Ringeval and V. Vennin
Reference: arXiv:1609.04739
The Cosmic Microwave Background radiation (CMB) is an amazingly simple and beautiful picture that is pivotal for observational cosmology. It is the oldest light in our Universe: it originates from when the Universe was only a sprightly 380,000 years old, much younger than its current 13.8 billion years. Cosmologists can measure this radiation to high precision and extract information about the early Universe. Specifically, they can learn about the epoch of inflation, which was a period of accelerated expansion in the first fractions of a second after the Big Bang.
There are hundreds of theoretical inflationary models that attempt to describe the physics of this epoch. All of them have slightly different predictions for the two important numbers, $latex \displaystyle n_s$ and $latex r$. The number $latex n_s$ measures the relative strength of cosmological perturbations with different wavelengths: if it is exactly equal to one, all perturbations have the same power, if it is smaller than one, the longer wavelengths have more power and if it is bigger than one, the smaller wavelengths have more power. $latex r$ is, loosely speaking, the ratio of primordial gravitational waves to the other primordial cosmological fluctuations. In other words, it measures how many gravitational waves were produced in the early universe as compared to what was around at that time.
Recent data from the Planck satellite have ruled out many models on the basis of these numbers, but a large class of scenarios remains compatible with the data. The hope is that future experiments will further restrict the number of allowed models to help us pinpoint what actually happened during inflation. One way to go about determining what the “correct” model of inflation is, is to systematically compare the predictions of each model with the data. However, a more efficient method is to have a model-independent parametrization of inflation so that you don’t have to specify your model, i.e. the particles and interactions, and then compute the values for $latex n_s$ and $latex r$ every time you change the model. There exist several of these model-independent descriptions of inflation: the truncated horizon-flow formalism, the hydrodynamical description of inflation and “universality classes” . The authors of this article argue that each of these approaches has serious shortcomings. Here I summarize the main drawbacks of the “universality classes”.
So what are universality classes? One can write $latex n_s$ and $latex r$ as a function of how much our universe expanded during the final phase of inflation, $latex \Delta N_*$ . $latex \Delta N_*$ is typically taken to be large, and thus $latex 1 / \Delta N_*$ is small. Therefore, the expressions for $latex n_s$ and $latex r$ can be expanded in terms of the smallness parameter $latex 1 / \Delta N_*$. Then it turns out that the leading order behavior falls into three classes:
- Perturbative, for which the leading order term shows power-law behavior;
- Non-perturbative, for which the leading order term is an exponential;
- Logarithmic, for which the leading order term is logarithmic in $latex \Delta N_*$.
When all these classes were introduced, the idea was that they allow a model-independent, systematic way to analyze the data. But we shall see that there are some issues with this approach.
First of all, it turns out that the three universality classes are not enough to describe all inflationary models. At leading order in the $latex 1/\Delta N_*$ expansion, a given model may fall into one of these classes, but at the next-to-leading order it can belong to a different class. For instance, consider the popular inflationary model called Starobinsky inflation. Starobinsky inflation is non-perturbative at leading order but logarithmic at the next. Thus, the three classes are not enough to classify all models and you need to increase the number of classes if you consider the next-to-leading order. This is not a problem by itself, but it this means that one of the attractive features of these universality classes (“you only need three classes”) is not true. Due to these higher order terms, you need to introduce new hybrid classes. The number of universality classes increases even more if you go to even higher orders. Now you may argue that this is only a theoretical issue and that the lowest order is more than enough to describe the data. But this is not the case, as you can see in Fig.1.: you need at least to go to the next order to get accurate predictions (especially for future CMB experiments).

Secondly, for many inflationary models if one were to apply the $latex 1/\Delta N_*$ expansion, one finds that the terms in the expansion depend on the parameters of the specific inflationary model. This is, in principle okay, but it can happen that the $latex 1/\Delta N_*$ expansion is only valid for a restrictive set of the parameter space. This can exclude the realistic values for the parameters of the model. So there are various inflationary scenarios for which one cannot even perform the $latex 1/\Delta N_*$ expansion! Thus, the ‘universality classes’ are not as universal as the name suggests.
Third, the $latex 1/\Delta N_*$ expansion is useful if you know a priori the allowed range of $latex \Delta N_*$. Typically, one assumes $latex \Delta N_* \in \left[ 50,60 \right]$ (or if you are slightly more conservative $latex \Delta N_* \in \left[ 40,70 \right]$). However, these values are only reasonable under specific conditions and depend sensitively on the period of reheating that follows inflation and the scale of inflation. For instance, one can even have $latex \Delta N_* =100$ in single-field inflation depending on the details of reheating. So for various models, $latex \Delta N_*$ falls outside the typically chosen range. This questions the usefulness of the $latex 1/\Delta N_*$ expansion given that one cannot predict the value of $latex \Delta N_*$ accurately.
Finally, and this may be even the strongest drawback of this model independent approach: it is statistically flawed. If you look for example at the perturbative class and you want to fit the data to:
$latex \epsilon = \beta (\Delta N_*)^{- \alpha} $
then you need to give a statistical prior for $latex \alpha$ and $latex \beta$. We may take a flat prior for these parameters. Now consider a particular model of inflation and reheating that falls within this universality class and is described by some parameters $latex \theta_1, \theta_2, \ldots \theta_n$. For this model, the parameters $latex \alpha$ and $latex \beta$ are functions of $latex \theta_1, \theta_2, \ldots \theta_n$ and assuming a flat prior for $latex \alpha$ and $latex \beta$ may induce a very funky prior for the parameters of the inflationary model $latex \theta_1, \theta_2, \ldots \theta_n$. Thus, from a statistical approach these universality classes are not particularly useful either as the introduce very unnatural priors on the parameters in the inflationary models it tries to describe.
Further reading
- Beautiful lecture notes on early universe cosmology and inflation by Daniel Baumann are available on his website
- Another set of great lecture notes by another expert in the field, Leonardo Senator, is also a good introduction to inflation and the CMB
- For more background on the universality classes, see the original articles referenced in the paper.




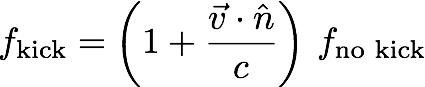

![Fig. 2: If a black hole binary radiates isotropically, it does not experience any kick and the gravitational wave has the black waveform. However, if it experiences a kick along the line of sight, the waveform can get redshifted (when the system moves away from us) as shown on the left of blueshifted (when system moves toward us) as shown on the right. The top and lower panel correspond to the two independent polarizations of the gravitational wave.[Figure taken from this paper]](http://www.particlebites.com/wp-content/uploads/2016/07/figure_redshiftedwave-300x107.jpg)