Posted on

SUSY vs. The Machines

Article title: Bayesian Neural Networks for Fast SUSY Predictions

Authors: B. S. Kronheim, M. P. Kuchera, H. B. Prosper, A. Karbo

Reference: https://arxiv.org/abs/2007.04506

It has been a while since we have graced these parts with the sounds of the attractive yet elusive superhero named SUSY. With such an arduous history of experimental effort, supersymmetry still remains unseen by the eyes of even the most powerful colliders. Though in the meantime, phenomenologists and theorists continue to navigate the vast landscape of model parameters with hopes of narrowing in on the most intriguing predictions – even connecting dark matter into the whole mess.

How vast you may ask? Well the ‘vanilla’ scenario, known as the Minimal Supersymmetric Standard Model (MSSM) – containing partner particles for each of those of the Standard Model – is chock-full of over 100 free parameters. This makes rigorous explorations of the parameter space not only challenging to interpret, but also computationally expensive. In fact, the standard practice is to confine oneself to a subset of the parameter space, using suitable justifications, and go ahead to predict useful experimental observables like collider production rates or particle masses. One of these popular motivations is known as the phenoneological MSSM (pMSSM), which reduces the huge parameter area to just less than 20 by assuming the absence of things like SUSY-driven CP-violation, flavour changing neutral currents (FCNCs) and differences between first and second generation SUSY particles. With this in the toolbox, computations become comparatively more feasible, with just enough complexity to make solid but interesting predictions.

But even coming from personal experience, these spaces can still be typically be rather tedious to work through – especially since many parameter selections are theoretically nonviable and/or in disagreement with previously well-established experimental observables, like the mass of the Higgs Boson. Maybe there is a faster way?

Machine learning has shared a successful history with a lot of high-energy physics applications, particularly those with complex dynamics like SUSY. One particularly useful application, at which machine learning is very accomplished at, is classification of points as excluded or not excluded based on searches at the LHC by ATLAS and CMS.

In the considered paper, a special type of Neural Network (NN) known as a Bayesian Neural Network (BNN) is used, which notably rely on probablistic certainty of classification rather than simply classifying a result as one thing or the other.

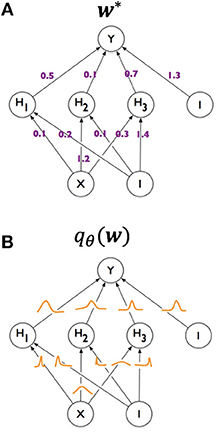
Figure 1: Your standard Neural Network (NN) shown in A has a single weight for each of its neuron connections (just represented by a number), learned from the training set. However, a Bayesian Neural Network (BNN) represented in B instead has a posterior distribution for each weight. When trained, it takes a prior distribution and applies Bayesian methods to obtain a posterior distribution. Taken from https://doi.org/10.3389/fninf.2019.00067.

In a typical NN there is a space of adjustable parameters (often called “features”) and a list of “targets” for the model to learn classification from. In this particular case, the model parameters are of course the features to learn from – these mainly include mass parameters for the different superparticles in the spectrum. These are mapped to three different predictions or targets that can be computed from these parameters:

  1. The mass of the lightest, neutral Higgs Boson (the 125 GeV one)
  2. The cross sections of processes involving the superpartners to the elecroweak guage bosons (typically called the neutralinos and charginos – I will let you figure out which ones are the charged and neutral ones)
  3. Whether the point is actually valid or not (or maybe theoretically consistent is a better way to put it).

Of course there is an entire suite of programs designed to carry out these calculations, which are usually done point by point in the parameter space of the pMSSM, and hence these would be used to construct the training data sets for the algorithm to learn from – one data set for each of the predictions listed above.

But how do we know our model is trained properly once we have finished the learning process? There are a number of metrics that are very commonly used to determine whether a machine learning algorithm can correctly classify the results of a set of parameter points. The following table sums up the four different types of classifications that could be made on a set of data.

Table 1: Classifications for data given the predicted and actual results.

The typical measures employed using this table are the precision, recall and F1 score which are in practice readily defined as:

P = \frac{TP}{TP+FP}, \quad R = \frac{TP}{TP+FN}, \quad F_1 = 2\frac{P \cdot R}{P+R}.

In predicting the validity of points, the recall especially will tell us the fraction of valid points that will be correctly identified by the algorithm. For example, the metrics for this validity data set are shown in Table 2.

Table 2: Metrics for point validity data set. A point is valid from the classifier if it exceeds a cutoff of 0.5 in the first row, with a more relaxed 3 standard deviations in the second.

With a higher Recall but lower precision for the 3 standard deviation cutoff it is clear that points with a larger uncertainty will be classified as valid in this case. Such a scenario would be useful in calculating further properties like the mass spectrum, but not neccesarily as the best classifier.

Similarly with the data set used to compute cross sections, the standard deviation can be used for points where the predictions are quite uncertain. On average their calculations revealed just over 3% percent error with the actual value of the cross section. Not to be outdone, in calculating the Higgs boson mass, within 2 GeV deviation of 125 GeV, the precision of the BNN was found to be 0.926 with a recall of 0.997, showing that very few parameter points that are actually conistent with the light neutral Higgs will actually be removed.

In the end, our whole purpose was to provide reliable SUSY predictions at a fraction of the time. It is well known that NNs provide relatively fast calculation, especially when utilizing powerful hardware, and in this case could acheive up to over 16 million times faster in computing a single point than standard SUSY software! Finally, it is worth to note that neural networks are highly scalable and so predictions from the 19-dimensional pMSSM are but one of the possibilities for NNs in calculating SUSY observables.

Futher Reading

[1] Bayesian Neural Networks and how they differ from traditional NNs: https://towardsdatascience.com/making-your-neural-network-say-i-dont-know-bayesian-nns-using-pyro-and-pytorch-b1c24e6ab8cd

[2] More on machine learning and A.I. and its application to SUSY: https://arxiv.org/abs/1605.02797

Posted on

A simple matter

Article title: Evidence of A Simple Dark Sector from XENON1T Anomaly

Authors: Cheng-Wei Chiang, Bo-Qiang Lu

Reference: arXiv:2007.06401

As with many anomalies in the high-energy universe, particle physicists are rushed off their feet to come up with new, and often somewhat often complicated models to explain them. With the recent detection of an excess in electron recoil events in the 1-7 keV region from the XENON1T experiment (see Oz’s post in case you missed it), one can ask whether even the simplest of models can even still fit the bill. Although still at 3.5 sigma evidence – not quite yet in the ‘discovery’ realm – there is still great opportunity to test the predictability and robustness of our most rudimentary dark matter ideas.

The paper in question considers would could be one of the simplest dark sectors with the introduction of only two more fundamental particles – a dark photon and a dark fermion. The dark fermion plays the role of the dark matter (or part of it) which communicates with our familiar Standard Model particles, namely the electron, through the dark photon. In the language of particle physics, the dark sector particles actually carries a kind of ‘dark charge’, much like the electron carries what we know as the electric charge. The (almost massless) dark photon is special in the sense that it can interact with both the visible and dark sector – and as opposed to visible photons, and have a very long mean free path able to reach the detector on Earth. An important parameter describing how much the ordinary and dark photon ‘mix’ together is usually described by \varepsilon. But how does this fit into the context of the XENON 1T excess?

Fig 1: Annihilation of dark fermions into dark photon pairs

The idea is that the dark fermions annihilate into pairs of dark photons (seen in Fig. 1) which excite electrons when they hit the detector material, much like a dark version of the photoelectric effect – only much more difficult to observe. The processes above remain exclusive, without annihilating straight to Standard Model particles, as long as the dark matter mass remains less than the lightest charged particle, the electron. With the electron at a few hundred keV, we should be fine in the range of the XENON excess.

What we are ultimately interested in is the rate at which the dark matter interacts with the detector, which in high-energy physics are highly calculable:

\frac{d R}{d \Delta E}= 1.737 \times 10^{40}\left(f_{\chi} \alpha^{\prime}\right)^{2} \epsilon(E)\left(\frac{\mathrm{keV}}{m_{\chi}}\right)^{4}\left(\frac{\sigma_{\gamma}\left(m_{\chi}\right)}{\mathrm{barns}}\right) \frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{\left(E-m_{\chi}\right)^{2}}{2 \sigma^{2}}}

where f_{\chi} is the fraction of dark matter represented by \chi, \alpha'=\varepsilon e^2_{X} / (4\pi), \epsilon(E) is the efficiency factor for the XENON 1T experiment and \sigma_{\gamma} is the photoelectric cross section.

Figure 2 shows the favoured regions for the dark fermion explanation fot the XENON excess. The dashed green lines represent only a 1% fraction of dark fermion matter for the universe, whilst the solid lines are to explain the entire dark matter content. Upper limits from the XENON 1T data is shown in blue, with a bunch of other astrophysical contraints (namely red giants, red dwarfs and horizontal branch star) far above the preffered regions.

Fig 2: The green bands represent the 1 and 2 sigma parameter regions in the \alpha' - m_{\chi} plane favoured by the dark fermion model in explaning the XENON excess. The solid lines cover the entire DM component, whilst the dashed lines are only a 1% fraction.

This plot actually raises another important question: How sensitive are these results to the fraction of dark matter represented by this model? For that we need to specify how the dark matter is actually created in the first place – with the two most probably well-known mechanisms the ‘freeze-out’ and the ‘freeze-in’ (follow the links to previous posts!)

Fig 3: Freeze-out and freeze-in mechanisms for producing the dark matter relic density. The measured density (from PLANCK) is \Omega h^2 = 0.12, shown on the red solid curve. The best fit values are also shown by the dashed lines, with their 1 sigma band. The mass of the dark fermion is fixed to its best-fit value of 3.17 keV, from Figure 2.

The first important point to note from the above figures is that the freeze-out mechanism doesn’t even depend on the mixing between the visible and dark sector i.e. the vertical axes. However, recall that the relic density in freeze-out is determined by the rate of annihlation into SM fermions – which is of course forbidden here for the mass of fermionic DM. The freeze-in works a little differently since there are two processes that can contribute to populating the relic density of DM: SM charged fermion annihlations and dark photon annihilations. It turns out that the charged fermion channel dominates for larger values of e_X and in of course then becomes insensitive to the mixing parameter \varepsilon and hence dark photon annihilations.

Of course it has been emphasized in previous posts that the only way to really get a good test of these models is with more data. But the advantage of simple models like these are that they are readily available in the physicist’s arsenal when anomalies like these pop up (and they do!)

Posted on

Are You Magnetic?

It’s no secret that the face of particle physics lies in the collaboration of scientists all around the world – and for the first time a group of 170 physicists have come to a consensus on one of the most puzzling predictions of the Standard Model muon. The anomalous magnetic moment of the muon concerns the particle’s rotation, or precession, in the presence of a magnetic field. Recall that elementary particles, like the electron and muon, possess intrinsic angular momentum, called spin, and hence indeed behave like a little dipole “bar magnet” – consequently affected by an external magnetic field.

The “classical” version of such an effect comes straight from the Dirac equation, a quantum mechanical framework for relativistic spin-1/2 particles like the electron and muon. It is expressed in terms of the g-factor, where g=2 in the Dirac theory. However, more accurate predictions, to compare to with experiment, require more extended calculations in the framework of quantum field theory, with “loops” of virtual particles forming the quantum mechanical corrections. In such a case we of course find deviation from the classical value in what becomes the anomalous magnetic moment with

a = \frac{g-2}{2}

For the electron, the prediction coming from Quantum Electrodynamics (QED) is so accurate, it actually agrees with the experimental result up to 10 significant figures (side note: in fact, this is not the only thing that agrees very well with experiment from QED, see precision tests of QED).

Figure 1: a “one-loop” contribution to the magnetic dipole moment in the theory of Quantum Electrodynamics (QED)

The muon, however, isn’t so simple and actually gets rather messy. In the Standard Model it comes with three parts, QED, electroweak and hadronic contributions

a^{SM}_{\mu} = a^{QED}_{\mu}+a^{EW}_{\mu}+a^{hadron}_{\mu}

Up until now, the accuracy of these calculations have been the subject of a number of collaborations around the world. The largest source (in fact, almost all) of the uncertainty actually comes from the smaller contributions to the magnetic moment, the hadronic part. It is so difficult to estimate that it actually requires input from experimental sources and lattice QCD methods. This review constitutes the most comprehensive report of both the data-driven and lattice methods for hadronic contributions to the muon’s magnetic moment.

Their final result, a^{SM}_{\mu} = 116591810(43) \times 10^{-11} remains 3.7 standard deviations below the current experimental value, measured at Fermilab in Brookhaven National Laboratory. However the most exciting part about all this is the fact that Fermilab is on the brink of releasing a new measurement, with the uncertainties reduced by almost a factor of four compared to the last. And if they don’t agree then? We could be that much closer to confirmation of some new physics in one of the most interesting of places!

References and Further Reading:

1. The new internationally-collaborated calculation: The anomalous magnetic moment of the muon in the Standard model, https://arxiv.org/abs/2006.04822

2. https://news.fnal.gov/2020/06/physicists-publish-worldwide-consensus-of-muon-magnetic-moment-calculation/

Posted on

Dark matter from down under

It isn’t often I get to plug an important experiment in high-energy physics located within my own vast country so I thought I would take this opportunity to do just that. That’s right – the land of the kangaroo, meat-pie and infamously slow internet (68th in the world if I recall) has joined the hunt for the ever elusive dark matter particle.

By now you have probably heard that about 85% of the universe is all made out of stuff that is dark. Searching for this invisible matter has not been an easy task, however the main strategy has involved detections of faint signals of dark matter scattering off nuclei that constantly pass through the Earth unimpeded. Up until now, the main contenders for these dark matter direct detection experiments have been performed above the equator.

The SABRE (Sodium-iodide with Active Background REjection) collaboration plans to operate two detectors – one in my home-state of Victoria, Australia at SUPL (Stawell Underground Physics Laboratory) and another in the northern hemisphere at LNGS, Italy. The choice to run two experiments in seperate hemispheres has the goal of potentially removing systematic effects inherent in the seasonal rotation of the Earth. In particular – any of these seasonal effects should be opposite in phase, whilst the dark matter signal should remain the same. This actually takes us to a novel dark matter direct detection search method known as annual modulation, which has been added to the spotlight through the DAMA/LIBRA scintillation detector underground the Laboratori Nazionali del Gran Sasso in Italy.

Around the world, around the world

Figure 1: When the Earth rotates around the sun, relative to the Milky Way’s DM halo, it experiences a larger interaction when it moves “head-on” with the wind. Taken from
arXiv:1209.3339.

The DAMA/LIBRA experiment superseded the DAMA/NaI experiment which observed the dark matter halo over a period of 7 annual cycles ranging from 1995 to 2002. The idea is quite simple really. Current theory suggests that the Milky Way galaxy is surrounded by a halo of dark matter with our solar system casually floating by experiencing some “flux” of particles that pass through us all year round. However, current and past theory (up to a point) also suggest the Earth does a full revolution around the sun in a year’s time. In fact, with respect to this dark matter “wind”, the Earth’s relative velocity would be added on its approach, occurring around the start of June and then subtracted on its recession, in December. When studying detector interactions with the DM particles, one would then expect the rates to be higher in the middle of the year and of course lower at the end – hence a modulation (annually). Up to here, annual modulation results would be quite suitably model-independent and so wouldn’t depend on your particular choice of DM particle – so long as it has some interaction with the detector.

The DAMA collaboration, having reported almost 14 years of annual modulation results in total, claim evidence for a picture quite consistent with what would be expected for a range of dark matter scenarios in the energy range of 2-6 keV. This however has long been in tension with the wider community of detection for WIMP dark matter. Those such as XENON (which incidentally is also located in the Gran Sasso mountains) and CDMS have reported no detection of dark matter in the same ranges as that which the DAMA collaboration claimed to have seen them. Although these employ quite different materials such as (you guessed it) liquid xenon in the case of XENON and cryogenically cooled semiconductors at CDMS.

Figure 2: Annual modulation results from DAMA. Could this be the presence of WIMP dark matter or some other seasonal effect? From the DAMA Collaboration.

Yes, there is also the COSINE-100 experiment, using the same materials as those in DAMA (that is, sodium iodide), based in South Korea. And yes, they also published a letter to Nature claiming their results to be in “severe tension” with those of the DAMA annual modulation signal – under the assumption of WIMP interactions that are spin-independent with the detector material. However, this does not totally rule out the observation of dark matter by DAMA – just the fact that it is very unlikely to correspond to the gold-standard WIMP in a standard halo scenario. According to the collaboration, it will certainly take years more data collection to know for sure. But that’s where SABRE comes in!

As above, so below

Before the arrival of SABRE’s twin detectors in both the northern and southern hemispheres, the first phase known as the PoP (Proof of Principle) must be performed to analyze the entire search strategy and evaluate the backgrounds present in the crystal structures. Certainly, another feature of SABRE is a crystal background rate quite below that of DAMA/LIBRA using ultra-radiopure sodium iodide crystals. With the estimated current background and 50 kg of detector material, it is expected that the DAMA/LIBRA signal should be able to be independently verified (or refuted) in a matter of 3 years.

If you asked me, there is something a little special about an experiment operating on the frontier of fundamental physics in a small regional Victorian town with a population just over 6000 known for an active gold mining community and the oldest running foot race in Australia. Of course, Stawell features just the right environment to shield the detector from the relentless bombardment of cosmic rays on the Earth’s surface – and that’s why it is located 1 km underground. In fact, radiation contamination is such a prevalent issue for these sensitive detectors that everything from the concrete to the metal bolts that go in them must first be tested – and all this at the same time as the mine is still being operated.

Now, not only is SABRE experiments running in both Australia and Italy, but they actually comprise a collaboration of physicists also from the UK and the USA. But most importantly (for me, anyway) – this is the southern hemisphere’s very first dark matter detector – a great milestone and a fantastic opportunity to put Aussies in the pilot’s seat to uncover one of nature’s biggest mysteries. But for now, crack open a cold one – footy’s almost on!

Figure 3: The SABRE collaboration operates internationally with detectors in the northern and southern hemispheres. Taken from GSSI.

References and Further Reading

  1. The SABRE dark matter experiment: https://sabre.lngs.infn.it/.
  2. The COSINE-100 experiment summarizing the annual modulation technique: https://cosine.yale.edu/about-us/annual-modulation-dark-matter.
  3. The COSINE-100 Experiment search for dark matter in tension with that of the DAMA signal: arXiv:1906.01791.
  4. An overview of the SABRE experiment and its Proof of Principle (PoP) deployment: arXiv:1807.08073.

Posted on

Does antihydrogen really matter?

Article title: Investigation of the fine structure of antihydrogen

Authors: The ALPHA Collaboration

Reference: https://doi.org/10.1038/s41586-020-2006-5 (Open Access)

Physics often doesn’t delay our introduction to one of the most important concepts in history – symmetries (as I am sure many fellow physicists will agree). From the idea that “for every action there is an equal and opposite reaction” to the vacuum solutions of electric and magnetic fields from Maxwell’s equations, we often take such astounding universal principles for granted. For example, how many years after you first calculated the speed of a billiard ball using conservation of momentum did you realise that what you were doing was only valid because of the fundamental symmetrical structure of the laws of nature? And hence goes our life through physics education – we first begin from what we ‘see’ to understanding what the real mechanisms are that operate below the hood.

These days our understanding of symmetries and how they relate to the phenomena we observe have developed so comprehensively throughout the 20th century that physicists are now often concerned with the opposite approach – applying the fundamental mechanisms to determine where the gaps are between what they predict and what we observe.

So far one of these important symmetries has stood up the test of time with no observable violation so far being reported. This is the simultaneous transformation of charge conjugation (C), parity (P) and time reversal (T), or CPT for short. A ‘CPT-transformed’ universe would be like a mirror-image of our own, with all matter as antimatter and opposite momenta. the amazing thing is that under all these transformations, the laws of physics behave the exact same way. With such an exceptional result, we would want to be absolutely sure that all our experiments say the same thing, so that brings us the our current topic of discussion – antihydrogen.

Matter, but anti.

Figure 1: The Hydrogen atom and its nemesis – antihydrogen. Together they are: Light. Source: Berkeley Science Review

The trick with antimatter is to keep it as far away from normal matter as possible. Antimatter-matter pairs readily interact, releasing vast amounts of energy proportional to the mass of the particles involved. Hence it goes without saying that we can’t just keep them sealed up in Tupperware containers and store them next to aunty’s lasagne. But what if we start simple – gather together an antiproton and a single positron and voila, we have antihydrogen – the antimatter sibling to the most abundant element in nature. Well this is precisely what the international ALPHA collaboration at CERN has been concerned with, providing “slowed-down” antiprotons with positrons in a device known as a Penning trap. Just like hydrogen, the orbit of a positron around an antiproton behaves like a tiny magnet, a property known as an object’s magnetic moment. The difficulty however is in the complexity of external magnetic field required to ‘trap’ the neutral antihydrogen in space. Therefore not surprisingly, these are the atoms of very low kinetic energy (i.e. cold) that cannot overcome the weak effect of external magnetism.

There are plenty more details of how the ALPHA collaboration acquires antihydrogen for study. I’ll leave this up to a reference at the end. What I’ll focus on is what we can do with it and what it means for fundamental physics. In particular, one of the most intriguing predictions of the invariance of the laws of physics under charge, parity and time transformations is that antihydrogen should share many of the same properties as hydrogen. And not just the mass and magnetic moment, but also the fine structure (atomic transition frequencies). In fact, the most successful theory of the 20th century, quantum electrodynamics (QED), properly accomodating anti-electronic interactions, also predicts a foundational test for both matter and antimatter hydrogen – the splitting of the 2S_{1/2} and 2P_{1/2} energy levels (I’ll leave a reference to a refresher on this notation). This is of course known as the Nobel-Prize winning Lamb Shift in hydrogen, a feature of the interaction between the quantum fluctuations in the electromagnetic field and the orbiting electron.

I’m feelin’ hyperfine

Of course it is only very recently that atomic versions of antimatter have been able to be created and trapped, allowing researchers to uniquely study the foundations of QED (and hence modern physics itself) from the perspective of this mirror-reflected anti-world. Very recently, the ALPHA collaboration have been able to report the fine structure of antihydrogen up to the n=2 state using laser-induced optical excitations from the ground state and a strong external magnetic field. Undergraduates by now will have seen, at least even qualitatively, that increasing the strength of an external magnetic field on an atomic structure also increases the gaps in the energy levels, and hence frequencies of their transitions. Maybe a little less known is the splitting due to the interaction between the electron’s spin angular momentum and that of the nucleus. This additional structure is known as the hyperfine structure, and is readily calculable in hydrogen utilizing the 1/2-integer spins of the electron and proton.

Figure 2: The expected energy levels in the antimatter version of hydrogen, an antiproton with an orbiting positron. Increased splitting on the x-axis are shown as a function of external magnetic field strength, a phenomena well-known in hydrogen (and thus predicted in antihydrogen) as the Zeeman Effect. The hyperfine splitting, due to the interaction between the positron and antiproton spin alignment are also shown by the arrows in the kets, respectively.

From the predictions of QED, one would expect antihydrogen to show precisely this same structure. Amazingly (or perhaps exactly as one would expect?) the average measurement of the antihydrogen transition frequencies agree with those in hydrogen to 16 ppb (parts per billion) – an observation that solidly keeps CPT invariance in rule but also opens up a new world of precision measurement of modern foundational physics. Similarly, with consideration to the Zeeman and hyperfine interactions, the splitting between 2P_{1/2} - 2P_{3/2} is found to be consistent with the CPT invariance of QED up to a level of 2 percent, and the identity of the Lamb shift (2S_{1/2} - 2P_{1/2}) up to 11 percent. With advancements in antiproton production and laser inducement of energy transitions, such tests provide unprecedented insight into the structure of antihydrogen. The presence of an antiproton and more accurate spectroscopy may even help in answering the unsolved question in physics: the size of the proton!

Figure 3: Transition frequencies observed in antihydrogen for the 1S-2P states (with various spin polarizations) compared with the theoretical expectation in hydrogen. The error bars are shown to 1 standard deviation.

References

  1. A Youtube link to how the ALPHA experiment acquires antihydrogen and measures excitations of anti-atoms: http://alpha.web.cern.ch/howalphaworks
  2. A picture of my aunty’s lasagne: https://imgur.com/a/2ffR4C3
  3. A reminder of what that fancy notation for labeling spin states means: https://quantummechanics.ucsd.edu/ph130a/130_notes/node315.html
  4. Details of the 1) Zeeman effect in atomic structure and 2) Lamb shift, discovery and calculation: 1) https://en.wikipedia.org/wiki/Zeeman_effect 2) https://en.wikipedia.org/wiki/Lamb_shift
  5. Hyperfine structure (great to be familiar with, and even more interesting to calculate in senior physics years): https://en.wikipedia.org/wiki/Hyperfine_structure
  6. Interested about why the size of the proton seems like such a challenge to figure out? See how the structure of hydrogen can be used to calculate it: https://en.wikipedia.org/wiki/Proton_radius_puzzle
Posted on

The neutrino from below

Article title: The ANITA Anomalous Events as Signatures of a Beyond Standard Model Particle and Supporting Observations from IceCube

Authors: Derek B. Fox, Steinn Sigurdsson, Sarah Shandera, Peter Mészáros, Kohta Murase, Miguel Mostafá, and Stephane Coutu 

Reference: arXiv:1809.09615v1

Neutrinos have arguably made history for being nothing other than controversial. In fact from their very inception, their proposal by Wolfgang Pauli was described in his own words as “something no theorist should ever do”. Years on, as we established the role that neutrinos played in the processes of our sun, it was then discovered that it simply wasn’t providing enough of them. In the end the only option was to concede that neutrinos were more complicated than we ever thought, opening up a new area of study of ‘flavor oscillations’ with the consequence that they may in fact possess a small, non-zero mass – to this day yet to be explained.

On a more recent note, neutrinos have sneakily raised eyebrows with a number of other interesting anomalies. The OPERA collaboration, founded between CERN in Geneva, Switzerland and Gran Sasso, Italy, made international news with reports that their speeds exceeded the speed of light. Such an observation would certainly shatter the very foundations of modern physics and so was met with plenty of healthy skepticism. Alas it was eventually traced back to a faulty timing cable and all was right with the world again. However this has not been the last time that neutrinos have been involved in another controversial anomaly.

The NASA-involved Antarctic Impulsive Transient Antenna (ANITA) is an experiment designed to search for very, very energetic neutrinos originating from outer space. As the name also suggests, the experiment consists of a series of radio antennae contained in a balloon floating above the southern Antarctic ice. Very energetic neutrinos can in fact produce intense radio wave signals when they pass through the Earth and scatter off atoms in the Antarctic ice. This may sound strange, as neutrinos are typically referred to as ‘elusive’, however at incredibly high energies their probability of scattering increases dramatically – to the point where the Earth is ‘opaque’ to these neutrinos.

ANITA typically searches for the electromagnetic components of cosmic rays in the atmosphere, reflecting off the ice surface and subsequently inverting the phase of the radio wave. Alternatively, a small number of events can occur in the direction of the horizon, without reflecting off the ice and hence not inverting the waveform. However, physicists were surprised to find signals originating from below the ice, without phase inversion, in a direction much too steep to originate from the horizon.

Why is this a surprise you may ask? Well any particle present in the SM at these energies would have trouble traversing such a long distance throughout the Earth, measured in one of the observations with a chord length of 5700 km, whereas a neutrino would be expected to only survive a few hundred km. Such events would be expected to be mainly involving \nu_{\tau} (tau neutrinos), since these have the potential to convert to a charged tau lepton shortly before arriving and hadronising into an air shower, which is simply not possible for electrons or muons which are absorbed by the ice in a much smaller distance. But even in the case of tau neutrinos, the probability of such an event occuring with the observed trajectory is very small (below one in a million), leading physicists to explore more exotic (and exciting) options.

A simple possibility is that the ultra-high energy neutrinos coming from space could interact within the Earth to produce a BSM (Beyond Standard Model) particle that passes through the Earth until it exits and decays back to an SM lepton and then hadronizes in a shower of particles. Such a situation is shown in Figure 1, where the BSM particle comes from the well-known and popular supersymmetric SM extension, known as the stau slepton \tilde{\tau}.

Figure 1: An ultra-high energy neutrino interacting within the Earth to produce a beyond Standard Model particle before decaying back to a charged lepton and hadronizing, leaving a radio signal for ANITA. From “Tests of new physics scenarios at neutrino telescopes” talk by Bhavesh Chauhan.

In some popular supersymmetric extensions to the Standard Model, the stau slepton is typically the next-to-lightest supersymmetric particle (or NLSP) and can in fact be quite long-lived. In the presence of a nucleus, the stau may convert to the tau lepton and the LSP, which is typically the neutralino. In the paper titled above, the stau NLSP \tilde{\tau}_R can exist within the Gauge-Mediated Supersymmetry Breaking Model (GMSB) and can be produced through ultra-high energy neutrino interactions with nucleons with a not-so-tiny branching ratio of BR \lesssim 10^{-4}. Of course the tension still remains for the direct observation of staus that can fit resonably within this scenario, but the prospects of observing effects of BSM physics without the efforts of expensive colliders.

But the attempts at new physics explanations don’t end there. There are some ideas that involve the decays of very heavy dark matter candidates in the galactic Milky-Way center. In a similar vein, another possibility comes form the well-motivated sterile neutrino – a BSM candidate to explain the small, non-zero mass of the neutrino. There are a number of explanations for a large flux of sterile neutrinos throughout the Earth, however the rate at which they interact with the Earth is much more suppressed than the light “active” neutrinos. It could be then hoped that they would make their passage to the ANITA detector after converting back to a tau lepton.

Anomalies like these come and go, however in any case, physicists remain interested in alternate pathways to new physics – or even a motivation to search in a more specific region with collider technology. But collecting more data first always helps!

References and further reading:

Posted on

Riding the wave to new physics

Article title: “Particle physics applications of the AWAKE acceleration scheme”

Authors: A. Caldwell, J. Chappell, P. Crivelli, E. Depero, J. Gall, S. Gninenko, E. Gschwendtner, A. Hartin, F. Keeble, J. Osborne, A. Pardons, A. Petrenko, A. Scaachi , and M. Wing

Reference: arXiv:1812.11164

On the energy frontier, the search for new physics remains a contentious issue – do we continue to build bigger, more powerful colliders? Or is this a too costly (or too impractical) an endeavor? The standard method of accelerating charged particles remains in the realm of radio-frequency (RF) cavities, possessing an electric field strength of about 100 Megavolts per meter, such as that proposed for the future Compact Linear Accelerator (CLIC) at CERN aiming for center-of-mass energies in the multi-TeV regime. Such a technology in the linear fashion is nothing new, being a key part of the SLAC National Accelerator Laboratory (California, USA) for decades before it’s shutdown around the early millennium. However, a device such as CLIC would still require more than ten times the space of SLAC, predicted to come in at around 10-50 km. Not only that, the walls of the cavities are based on normal conducting material and so tend to heat up very quickly and so are typically run in short pulses. And we haven’t even mentioned the costs yet!

Physicists are a smart bunch, however, and they’re always on the lookout for new technologies, new techniques and unique ways of looking at the same problem. As you may have guessed already, the limiting factor determining the length required for sufficient linear acceleration is the field gradient. But what if there were a way to achieve hundreds of times that of a standard RF cavity? The answer has been found in plasma wakefields – separated bunches of dense protons with the potential to drive electrons up to gigaelectronvolt energies in a matter of meters!

Wakefields of plasma are by no means a new idea, being proposed first at least four decades ago. However, most examples have demonstrated this idea using electrons or lasers to ‘drive’ the wakefield in the plasma. More specifically, this is known as the ‘drive beam’ which does not actually participate in the acceleration but provides the large electric field gradient for what is known as the ‘witness beam’ – the electrons. However, this has not been demonstrated using protons as the drive beam to penetrate much further into the plasma – until now.

In fact, very recently CERN has demonstrated proton-driven wakefield technology for the first time during the 2016-2018 run of AWAKE (which stands for Advanced Proton Driven Plasma Wakefield Acceleration Experiment, naturally), accelerating electrons to 2 GeV in only 10 m. The protons that drive the electrons are injected from the Super Proton Synchrotron (SPS) into a Rubidium gas, ionizing the atoms and altering their uniform electron distribution into an osscilating wavelike state. The electrons that ‘witness’ the wakefield then ‘ride the wave’ much like a surfer at the forefront of a water wave. Right now, AWAKE is just a proof of concept, however plans to scale up to 10 GeV electrons in the coming years could hopefully pave the pathway to LHC level proton energies – shooting electrons up to TeV energies!

Figure 1: A layout of AWAKE (Advanced Proton Driven Plasma Wakefield Acceleration Experiment).

In this article, we focus instead on the interesting physics applications of such a device. Bunches of electrons with energies up to TeV energies is so far unprecedented. The most obvious application would of course be a high energy linear electron-positron collider. However, let’s focus on some of the more novel experimental applications that are being discussed today, particularly those that could benefit from such a strong electromagnetic presence in almost a ‘tabletop physics’ configuration.

Awake in the dark

One of the most popular considerations when it comes to dark matter is the existence of dark photons, mediating interactions between dark and visible sector physics (see “The lighter side of Dark Matter” for more details). Finding them has been the subject of recent experimental and theoretical approaches, even with high-energy electron fixed-target experiments already. Figure 2 shows such an interaction, where A^\prime represents the dark photon. One experiment based at CERN known as the NA64 already searches for dark photons through incident electrons on a target, utilizing interactions of the SPS proton beam. In the standard picture, the dark photon is searched through the missing energy signature, leaving the detector without interacting but escaping with a portion of the energy. The energy of the electrons is of course not the issue when the SPS is used, however the number of electrons is.

Figure 2: Dark photon production from a fixed-target experiment with an electron-positron final state.

Assuming one could work with the AWAKE scheme, one could achieve numbers of electrons on target orders of magnitude larger – clearly enhancing the reach for masses and mixing of the dark photon. The idea would be to introduce a high number of energetic electron bunches to a tungsten target with a following 10 m long volume for the dark photon to decay (in accordance with Figure 2). Because of the opposite charges of the electron and positron, the final decay products can then be separated with magnetic fields and hence one can ultimately determine the dark photon invariant mass.

Figure 3 shows how much of an impact a larger number of on-target electrons would make for the discovery reach in the plane of kinetic mixing \epsilon vs mass of the dark photon m_{A^\prime} (again we refer the reader to “The lighter side of Dark Matter” for explanations of these parameters). With the existing NA64 setup, one can already see new areas of the parameter space being explored for 1010 – 1013 electrons. However a significant difference can be seen with the electron bunches provided by the AWAKE configuration, with an ambitious limit shown by the 1016 electrons at 1 TeV.

Figure 3: Exclusion limits in the \epsilon - m_{A^\prime} plane for the dark photon decaying to an electron-positron final state. The NA64 experiment using larger numbers of electrons is shown in the colored non-solid curves from 1010 to 1013 of total on-target electrons. The solid colored lines show the AWAKE provided electron bunches with 1015 and 1016 at 50 GeV and 1016 at 1 TeV.

Light, but strong

Quantum Electrodynamics (or QED, for short), describing the interaction between fundamental electrons and photons, is perhaps the most precisely measured and well-studied theory out there, showing agreement with experiment in a huge range of situations. However, there are some extreme phenomena out in the universe where the strength of certain fields become so great that our current understanding starts to break down. For the electromagnetic field this can in fact be quantified as the Schwinger limit, above which it is expected that nonlinear field effects start to become significant. Typically at a strength around 1018 V/m, the nonlinear corrections to the equations of QED would predict the appearance of electron-positron pairs spontaneously created from such an enormous field.

One of the predictions is the multiphoton interaction with electrons in the initial state. In linear QED, the standard 2 \rightarrow 2 scattering of e^- + \gamma \rightarrow e^- + \gamma for example is only possible. In a strong field regime, however, the initial state can then open up to n numbers of photons. Given a strong enough laser pulse, multiple laser photons can interact with electrons and investigate this incredible region of physics. We show this in Figure 4.

Figure 4: Multiphoton interaction with an electron (left) and electron-positron production from photon absorption (right). $\latex n$ here is the number of photons absorbed in the initial state.

The good and bad news is that this had already been performed as far back as the 90s in the E144 experiment at SLAC, using 50 GeV electron bunches – however unable to reach the critical field value in the electrons frame of rest. AWAKE could certainly provide highly energetic electrons and allow for different kinematic experimental reach. Could this provide the first experimental measurement of the Schwinger critical field?

Of course, these are just a few considerations amongst a plethora of uses for the production of energetic electrons over such short distances. However as physicists desperately continue their search for new physics, it may be time to consider the use of new acceleration technologies on a larger scale as AWAKE has already shown its scalability. Wakefield acceleration may even establish itself with a fully-developed new physics search plan of its own.

References and further reading:

Posted on

Quark nuggets of wisdom

Article title: “Dark Quark Nuggets”

Authors: Yang Baia, Andrew J. Long, and Sida Lu

Reference: arXiv:1810.04360

Information, gold and chicken. What do they all have in common? They can all come in the form of nuggets. Naturally one would then be compelled to ask: “what about fundamental particles? Could they come in nugget form? Could that hold the key to dark matter?” Lucky for you this has become the topic of some ongoing research.

A ‘nugget’ in this context refers to large macroscopic ‘clumps’ of matter formed in the early universe that could possibly survive up until the present day to serve as a dark matter candidate. Much like nuggets of the edible variety, one must be careful to combine just the right ingredients in just the right way. In fact, there are generally three requirements to forming such an exotic state of matter:

  1. (At least) two different vacuum states separated by a potential ‘barrier’ where a phase transition occurs (known as a first-order phase transition).
  2. A charge which is conserved globally which can accumulate in a small part of space.
  3. An excess of matter over antimatter on the cosmological scale, or in other words, a large non-zero macroscopic number density of global charge.

Back in the 1980s, before much work was done in the field of lattice quantum chromodynamics (lQCD), Edward Witten put forward the idea that the Standard Model QCD sector could in fact accommodate such an exotic form of matter. Quite simply this would occur at the early phase of the universe when the quarks undergo color confinement to form hadrons. In particular Witten’s were realized as large macroscopic clumps of ‘quark matter’ with a very large concentration of baryon number, N_B > 10^{30}. However, with the advancement of lQCD techniques, the phase transition in which the quarks become confined looks more like a continuous ‘crossover’ (i.e. a second-order phase transition), making the idea in the Standard Model somewhat unfeasible.

Theorists, particularly those interested in dark matter, are not confined (for lack of a better term) to the strict details of the Standard Model and most often look to the formation of sometimes complicated ‘dark sectors’ invisible to us but readily able to provide the much needed dark matter candidate.

Dark QCD?

The problem of obtaining a first-order phase transition to form our quark nuggets need not be a problem if we consider a QCD-type theory that does not interact with the Standard Model particles. More specifically, we can consider a set of dark quarks, dark gluons with arbitrary characteristics like masses, couplings, numbers of flavors or numbers of colors (which of course are quite settled for the Standard Model QCD case). In fact, looking at the numbers of flavors and colors of dark QCD in Figure 1, we can see in the white unshaded region a number of models that can exist with a first-order phase transition, as required to form these dark quark nuggets.

Figure 1: The white unshaded region corresponds to dark QCD models which may permit a first-order phase transition and thus the existence of ‘dark quark nuggets’.

As with normal quarks, the distinction between the two phases actually refers to a process known as chiral symmetry breaking. When the temperature of the universe cools to this particular scale, color confinement of quarks occurs around the same time, such that no single-color quark can be observed on its own – only in colorless bound states.

Forming a nugget

As we have briefly mentioned so far, the dark nuggets are formed as the universe undergoes a ‘dark’ phase transition from a phase where the dark color is unconfined to a phase where it is confined. At some critical temperature, due to the nature of first-order phase transitions, bubbles of the new confined phase (full of dark hadrons) begin to nucleate out of the dark quark-gluon plasma. The growth of these bubbles are driven by a difference in pressure, characteristic of the fact that the unconfined and confined phase vacuums states are of different energy. With this emerging bubble wall, the almost massless particles from the dark plasma scatter from the wall containing heavy dark (anti)baryons and hence a large amount of dark baryon number accumulates in this phase. Eventually, as these bubbles merge and coalesce, we would expect local regions of remaining dark quark-gluon plasma, unconfined and stable from collapse due to the Fermi degeneracy pressure (see reference below for more on this). An illustration is shown in Figure 2. Calculations with varying energy scales of confinement estimate their masses are anywhere between 10^{-7} to 10^{23} grams with radii from 10^{-15} to 10^8 cm and so can truly be classed as macroscopic dark objects!

Figure 2: Dark Quark Nuggets are a phase of unconfined dark quark-gluon plasma kept stable by the balance between Fermi degeneracy pressure and vacuum pressure from the separation between the unconfined and confined phases.

How do we know they could be there? 

There are a number of ways to infer the existence of dark quark nuggets, but two of the main ones are: (i) as a dark matter candidate and (ii) through probes of the dark QCD model that provides them. Cosmologically, the latter can imply the existence of a dark form of radiation which ultimately can lead to effects on the Cosmic Microwave Background Radiation (CMB). In a similar vein, one recent avenue of study today is the production of a steady background of gravitational waves emerging from the existence of a first-order phase transition – one of the key requirements for dark quark nugget formation. More importantly, they can be probed through astrophysical means if they share some coupling (albeit small) with the Standard Model particles. The standard technique of direct detection with Earth-based experiments could be the way to go – but furthermore, there may be the possibility of cosmic ray production from collisions of multiple dark quark nuggets. Among these are a number of other observations over the massive range of nugget sizes and masses shown in Figure 3.

Figure 3: Range of dark quark nugget masses and sizes and their possible detection methods.

To conclude, note that in such a generic framework, a number of well-motivated theories may predict (or in fact have unavoidable) instances of quark nuggets that may serve as interesting dark matter candidates with a lot of fun phenomenology to play with. It is only up to the theorist’s imagination where to go from here!

References and further reading:

Posted on

The lighter side of Dark Matter

Article title: “Absorption of light dark matter in semiconductors”

Authors: Yonit Hochberg, Tongyan Lin, and Kathryn M. Zurek

Reference: arXiv:1608.01994

Direct detection strategies for dark matter (DM) have grown significantly from the dominant narrative of looking for scattering of these ghostly particles off of large and heavy nuclei. Such experiments involve searches for the Weakly-Interacting Massive Particles (WIMPs) in the many GeV (gigaelectronvolt) mass range. Such candidates for DM are predicted by many beyond Standard Model (SM) theories, one of the most popular involving a very special and unique extension called supersymmetry. Once dubbed the “WIMP Miracle”, these types of particles were found to possess just the right properties to be suitable as dark matter. However, as these experiments become more and more sensitive, the null results put a lot of stress on their feasibility.

Typical detectors like that of LUX, XENON, PandaX and ZEPLIN, detect flashes of light (scintillation) from the result of particle collisions in noble liquids like argon or xenon. Other cryogenic-type detectors, used in experiments like CDMS, cool semiconductor arrays down to very low temperatures to search for ionization and phonon (quantized lattice vibration) production in crystals. Already incredibly successful at deriving direct detection limits for heavy dark matter, new ideas are emerging to look into the lighter side.

Recently, DM below the GeV range have become the new target of a huge range of detection methods, utilizing new techniques and functional materials – semiconductors, superconductors and even superfluid helium. In such a situation, recoils from the much lighter electrons in fact become much more sensitive than those of such large and heavy nuclear targets.

There are several ways that one can consider light dark matter interacting with electrons. One popular consideration is to introduce a new gauge boson that has a very small ‘kinetic’ mixing with the ordinary photon of the Standard Model. If massive, these ‘dark photons’ could also be potentially dark matter candidates themselves and an interesting avenue for new physics. The specifics of their interaction with the electron are then determined by the mass of the dark photon and the strength of its mixing with the SM photon.

Typically the gap between the valence and conduction bands in semiconductors like silicon and germanium is around an electronvolt (eV). When the energy of the dark matter particle exceeds the band gap, electron excitations in the material can usually be detected through a complicated secondary cascade of electron-hole pair generation. Below the band gap however, there is not enough energy to excite the electron to the conduction band, and so detection proceeds through low-energy multi-phonon excitations, with the dominant being the emission of two back-to-back phonons.

In both these regimes, the absorption rate of dark matter in the material is directly related to the properties of the material, namely its optical properties. In particular, the absorption rate for ordinary SM photons is determined by the polarization tensor in the medium, and in turn the complex conductivity, \hat{\sigma}(\omega)=\sigma_{1}+i \sigma_{2} , through what is known as the optical theorem. Ultimately this describes the response of the material to an electromagnetic field, which has been measured in several energy ranges. This ties together the astrophysical properties of how the dark matter moves through space and the fundamental description of DM-electron interactions at the particle level.

In a more technical sense, the rate of DM absorption, in events per unit time per unit target mass, is given by the following equation:

R=\frac{1}{\rho} \frac{\rho_{D M}}{m_{A^{\prime}}} \kappa_{e f f}^{2} \sigma_{1}

  • \rho – mass density of the target material
  • \rho_{DM} – local dark matter mass density (0.3 GeV/cm3) in the galactic halo
  • m_{A'} – mass of the dark photon particle
  • \kappa_{eff} – kinetic mixing parameter (in-medium)
  • \sigma_1 – absorption rate of ordinary SM photons

Shown in Figure 1, the projected sensitivity at 90% confidence limit (C.L.) for a 1 kg-year exposure of semiconductor target to dark photon detection can be almost an order of magnitude greater than existing nuclear recoil experiments. Dependence is shown on the kinetic mixing parameter and the mass of the dark photon. Limits are also shown for existing semiconductor experiments, known as DAMIC and CDMSLite with 0.6 and 70 kg-day exposure, respectively.

Figure 1. Projected reach of a silicon (blue, solid) and germanium (green, solid) semiconductor target at 90% C.L. for 1 kg-year exposure through the absorption of dark photons DM, kinetically mixed with SM photons. Multi-phonon excitations are significant for the sub-eV range, and electron excitations approximately over 0.6 and 1 eV (the size of the band gaps for germanium and silicon, respectively).

Furthermore, in the millielectronvolt-kiloelectronvolt range, these could provide much stronger constraints than any of those that currently exist from sources in astrophysics, even at this exposure. These materials also provide a novel way of detecting DM in a single experiment, so long as improvements are made in phonon detection.

These possibilities, amongst a plethora of other detection materials and strategies, can open up a significant area of parameter space for finally closing in on the identity of the ever-elusive dark matter!

References and further reading: