Reggie Bain

October 14, 2016October 14, 2016

Tracking the Jets to Monte Carlo

Article: Calculating Track-Based Observables for the LHC
Authors: Hsi-Ming Chang, Massimiliano Procura, Jesse Thaler, and Wouter J. Waalewijn
Reference: arXiv:1303.6637 [hep-ph]

With the LHC churning out hordes of data by the picosecond, theorists often have to work closely with experimentalists to test various theories, devise models, etc. In order to make sure they’re developing the right kinds of tools to test their ideas, theorists have to understand how experimentalists analyze their data.

One very simple example that’s relevant to the LHC involves the reconstruction of jets. Experimentalists often reconstruct jets from only the charged particles (such as $\pi^{\pm}$ ) they see in the detector while theorists generally do calculations where jets have both charged and neutral particles (such as $\pi^0$ , see my previous ParticleBites for a more general intro to jets). In order to compare predictions with experiment, someone is going to have to compromise. The concept of Track-Based Observables is an interesting example of a way of attacking the more general problem of connecting the blackboard with accelerator.

Before diving into the details, let’s briefly look at the basics of how theorists and experimentalists make predictions about these trouble-making collimated sprays of radiation.

Figure 1: A basic diagram of different parts of the ATLAS detector. Note, in particular, what's being measured at the calorimetry and tracking stages. — Figure 1: A basic diagram of different parts of the ATLAS detector. Note, in particular, what’s being measured at the calorimetry and tracking stages.

Experiment: For experimentalists, jets are collections of clustered signatures left on the detector. These signatures generally come from calorimetry (i.e. measure the energy deposits) and/or from tracking where the trajectories (i.e. the kinematics) of final state particles are measured. At the LHC, where luminosities are absurdly high, a phenomenon known as “pileup” becomes an increasingly aggravating contaminant in the data. In short, pile-up is caused by the fact that the LHC isn’t just shooting a single proton at another proton in the beam, its shooting bunches of protons at each other. Of course while this makes the likelihood of a direct proton-proton collision more likely, it also causes confusion when looking at the mess of final state particles. How do you know which tracks of particles came from a given collision? It turns out that since measuring particle tracks gives you the kinematic properties of particles, those particles are much easier to deal with. However, neutral particles aren’t detected via tracking at the LHC, only via calorimetry. Thus, to make their lives significantly easier, experimentalists can simply do their analyses and reconstruct jets using purely the charged particles.

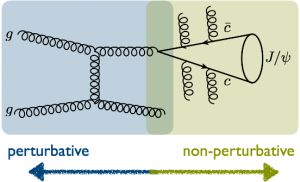
Theory: The notion of ignoring charged particles in the name of convenience doesn’t immediately jive with theorists. When using standard Quantum Field Theoretic (QFT) techniques to make predictions about jets, theorists have to turn back the clock on the zoo of final state particles that experimentalists analyze. For most sane theorists, calculations that involve 1 particle splitting into 2 is about all we generally tackle using perturbative QFT. Depending on the circumstances, calculating things at this stage is usually said to be a “next-to-leading order” or NLO calculation when one is using perturbation theory to describe strong interactions. This is because there is a factor of the strong coupling constant $\alpha_s$ multiplying this piece of whatever expression you’re dealing with. Luckily, it turns out that in QCD, this is largely all you need most of the time to make decent predictions. The tricky part is then turning a prediction about 1 particle splitting into 2 into a prediction about those particles splitting into 4 then 8 and so on, i.e. a fully hadronized and realistic event. For this, theorists generally employ hadronization “models” that are found by fitting to data or events simulated by Monte Carlo event generators. But how do you do this fitting? How can you properly separate physics into non-perturbative and perturbative pieces in a way that makes sense?

Figure 1: Theorists have to take parton-level predictions that can be reasonably calculated analytically using perturbative-QCD (or an effective theory) and using a combination of tools, turn these calculations into predictions about fully hadronized events. This diagram shows an example of a single parton hadronizing into many final state particles. The 1->2 splitting is calculated in perturbation theory. The second stage, which involves various q->qg, g->gg, etc. splittings (often referred to as "showering") is often obtained using something called "renormalization group evolution" which is beyond the scope of this bite. The final stage involves the actual fragmentation of partons into hadrons. This is where non-perturbative physics takes over and fits must often be done to Monte Carlo event generators or data. This diagram can be found in a fantastic talk by one of the paper's authors at https://goo.gl/2QlkSz. — Figure 2: Theorists have to take parton-level predictions that can be reasonably calculated analytically using perturbative-QCD (or an effective theory) and using a combination of tools, turn these calculations into predictions about fully hadronized events. This diagram shows an example of a single parton hadronizing into many final state particles. The 1->2 splitting is calculated in perturbation theory. The second stage, which involves various q->qg, g->gg, etc. splittings (often referred to as “showering”) is often obtained using something called “renormalization group evolution” which is beyond the scope of this bite. The final stage involves the actual fragmentation of partons into hadrons. This is where non-perturbative physics takes over and fits must often be done to Monte Carlo event generators or data. This diagram can be found in a fantastic talk by one of the paper’s authors at BOOST 2013.

The popular way of handling the tricky task of connecting NLO calculations with fully hadronized events is by using factorization theorems. What factorization theorems do, in short, is to compartmentalize analytic calculations into pieces involving physics happening at widely separated energy scales. Using perturbative techniques, we calculate relevant processes happening in each regime separately, and then combine those pieces as dictated by the factorization theorem to come up with a full answer. This oftentimes involves splitting up an observable into a perturbatively calculable piece and a non-perturbative piece that must be obtained via a fit to data or a Monte Carlo simulation.

Warning: These theorems are, in all but a few cases, not rigorously defined although there are many examples where factorization theorems can be shown to be true up to small power corrections in some parameter. This is often where the power of effective field theories is used. We’ll address this important and complex issue in future bites.
Where do track-based observables fit into all of this? Once we have a factorization theorem, we have to make sure that we encapsulate the physics in a systematic way that doesn’t have infinities popping up all over the place (as often happens when theorists aren’t careful). The authors of arXiv:1303.6637 define track functions that are combined with perturbatively calculable pieces via a factorization theorem they discuss to make an observable cross-section. To find the track functions, they fit their NLO analytic distributions for the fraction of the total jet energy carried by the jet’s charged particles to simulations done by PYTHIA.

Figure 3: The authors plot their analytic calculations combined with fitted track functions against results generated entirely from PYTHIA. Their results show that track functions can do a good job (up to smearing effects that PYTHIA's hadronization model imposes). — Figure 3: The authors plot their analytic calculations combined with fitted track functions against results generated entirely from PYTHIA. Their results show that track functions can do a good job (up to smearing effects that PYTHIA’s hadronization model imposes).

As can be seen in Figure 2, the authors then make predictions for a totally different observable using track functions combined with their analytic calculations and compare them to events generated entirely in PYTHIA, achieving very good results. Let’s take a second to appreciate how powerful an idea this is. By writing down the foundation for track functions, the authors have laid the groundwork for a host of track-based observables that focus specifically on probing the charged particles within a jet. However, the real impact is that these track functions are that they can be applied to any quarks/gluons that are undergoing fragmentation in any process. When these are eventually extracted from data at the LHC, phenomenologists will be able to perform analytic calculations and then, using track functions, make precision predictions about track-based observables that experimentalists can then use to more easily extract information about the structure of jets.

Further Reading

“Fragmentation and Hadronization,” by B.R. Webber of Cambridge/CERN. A concise and very clear introduction to the basics of how we model non-perturbative physics and the basic ideas behind how Monte Carlo event generators simulate fragmentation/hadronization.
“Factorization of Hard Processes in QCD”, by Collins, Soper, and Sterman. The grandaddy of papers on factorization by 3 giants in the field. Outlines the few existing proofs of factorization theorems.
“How a detector works,” A quick and very basic introduction to detectors used in particle physics.

August 23, 2016February 19, 2017

Jets aren’t just a game of tag anymore

Article: Probing Quarkonium Production Mechanisms with Jet Substructure
Authors: Matthew Baumgart, Adam Leibovich, Thomas Mehen, and Ira Rothstein
Reference: arXiv:1406.2295 [hep-ph]

“Tag…you’re it!” is a popular game to play with jets these days at particle accelerators like the LHC. These collimated sprays of radiation are common in various types of high-energy collisions and can present a nasty challenge to both theorists and experimentalists (for more on the basic ideas and importance of jet physics, see my July bite on the subject). The process of tagging a jet generally means identifying the type of particle that initiated the jet. Since jets provide a significant contribution to backgrounds at high energy colliders, identifying where they come from can make doing things like discovering new particles much easier. While identifying backgrounds to new physics is important, in this bite I want to focus on how theorists are now using jets to study the production of hadrons in a unique way.

Over the years, a host of theoretical tools have been developed for making the study of jets tractable. The key steps of “reconstructing” jets are:

Choose a jet algorithm (i.e. basically pick a metric that decides which particles it thinks are “clustered”),
Identify potential jet axes (i.e. the centers of the jets),
Decide which particles are in/out of the jets based on your jet algorithm.

Figure 1: A basic 3-jet event where one of the reconstructed jets is found to have been initiated by a b quark. The process of finding such jets is called "tagging." — Figure 1: A basic 3-jet event where one of the reconstructed jets is found to have been initiated by a b quark. The process of finding such jets is called “tagging.”

Deciphering the particle content of a jet can often help to uncover what particle initiated the jet. While this is often enough for many analyses, one can ask the next obvious question: how are the momenta of the particles within the jet distributed? In other words, what does the inner geometry of the jet look like?

There are a number of observables that one can look at to study a jet’s geometry. These are generally referred to as jet substructure observables. Two basic examples are:

Jet-shape: This takes a jet of radius R and then identifies a sub-jet within it of radius r. By measuring the energy fraction contained within sub-jets of variable radius r, one can study where the majority of the jet’s energy/momentum is concentrated.
Jet mass: By measuring the invariant mass of all of the particles in a jet (while simultaneously considering the jet’s energy and radius) one can gain insight into how focused a jet is.

Figure 2: A basic way to produce quarkonium via the fragmentation of a gluon. The interactions highlighted in blue are calculated using standard perturbative QCD. The green zone is where things get tricky and non-perturbative models that are extracted from data must be used. — Figure 2: A basic way to produce quarkonium via the fragmentation of a gluon. The interactions highlighted in blue are calculated using standard perturbative QCD. The green zone is where things get tricky and non-perturbative models that are extracted from data must often be used.

One way in which phenomenologists are utilizing jet substructure technology is in the study of hadron production. In arXiv:1406.2295, Baumgart et. al. introduced a way to connect the world of jet physics with the world of quarkonia. These bound states of charm-anti-charm or bottom-anti-bottom quarks are the source of two things: great buzz words for impressing your friends and several outstanding problems within the standard model. While we’ve been studying quarkonia such the $J/\psi(c\bar{c})$ and the $\Upsilon(b\bar{b})$ for a half-century, there are still a bunch of very basic questions we have about how they are produced (more on this topic in future bites).

This paper offers a fresh approach to studying the various ways in which quarkonia are produced at the LHC by focusing on how they are produced within jets. The wealth of available jet physics technology then provides a new family of interesting observables. The authors first describe the various mechanisms by which quarkonia are produced. In the formalism of Non-relativistic (NR) QCD, the $J/\psi$ for example, is most frequently produced at the LHC (see Fig. 2) when a high energy gluon splits into a $c\bar{c}$ pair in one of several possible angular momentum and color quantum states. This pair then ultimately undergoes non-perturbative (i.e. we can’t really calculate them using standard techniques in quantum field theory) effects and becomes a color-singlet final state particle (as any reasonably minded particle should do). While this model makes some sense, we have no idea how often quarkonia are produced via each mechanism.

Figure 3: This plot from arXiv:1406.2295 shows how the probability that a gluon or quark fragments into a jet with a specific energy E that a contains a $latex J/\psi$ with a fraction $latex z$ of the original quark/gluon's momentum varies for different mechanisms. The spectroscopic notation should be familiar from basic quantum mechanics. It gives the angular momentum and color quantum numbers of the $latex q\bar{q}$ pair that eventually becomes quarkonium. Notice that for different values of z and E, the different mechanisms behave differently. — Figure 3: This plot from arXiv:1406.2295 shows how the probability that a gluon or quark fragments into a jet with a specific energy E that a contains a $J/\psi$ with a fraction $z$ of the original quark/gluon’s momentum varies for different mechanisms. The spectroscopic notation should be familiar from basic quantum mechanics. It gives the angular momentum and color quantum numbers of the $q\bar{q}$ pair that eventually becomes quarkonium. Notice that for different values of z and E, the different mechanisms behave differently. Thus this observable (i.e. that mouth full of a probability distribution I described) is said to have *discriminating power* between the different channels by which a $J/\psi$ is typically formed.

Figure 3: This plot from arXiv:1406.2295 shows how the probability that a gluon or quark fragments into a jet with a specific energy E that a contains a $J/\psi$ with a fraction $z$ of the original quark/gluon’s momentum varies for different mechanisms. The spectroscopic notation should be familiar from basic quantum mechanics. It gives the angular momentum and color quantum numbers of the $q\bar{q}$ pair that eventually becomes quarkonium. Notice that for different values of z and E, the different mechanisms behave differently. Thus this observable (i.e. that mouth full of a probability distribution I described) is said to have *discriminating power* between the different channels by which a $J/\psi$ is typically formed.

This paper introduces a theoretical formalism that looks at the following question: what is the probability that a parton (quark/gluon) hadronizes into a jet with a certain substructure and that contains a specific hadron with some fraction $z$ of the original partons energy? The authors show that the answer to this question is correlated with the answer to the question: How often are quarkonia produced via the different intermediate angular-momentum/color states of NRQCD? In other words, they show that studying how the geometry of the jets that contain quarkonia may lead to answers to decades old questions about how quarkonia are produced!

There are several other efforts to study hadron production through the lens of jet physics that have also done preliminary comparisons with ATLAS/CMS data (one such study will be the subject of my next bite). These studies look at the production of more general classes of hadrons and numbers of jets in events and see promising results when compared with 7 TeV data from ATLAS and CMS.

The moral of this story is that jets are now being viewed less as a source of troublesome backgrounds to new physics and more as a laboratory for studying long-standing questions about the underlying nature of hadronization. Jet physics offers innovative ways to look at old problems, offering a host of new and exciting observables to study at the LHC and other experiments.

Further Reading

The November Revolution: https://www.slac.stanford.edu/history/pubs/gilmannov.pdf. This transcript of a talk provides some nice background on, amongst other things, the momentous discovery of the $J/\psi$ in 1974 what is often referred to the November Revolution.
An Introduction to the NRQCD Factorization Approach to Heavy Quarkonium https://cds.cern.ch/record/319642/files/9702225.pdf. As good as it gets when it comes to outlines of the basics of this tried-and-true effective theory. This article will definitely take some familiarity with QFT but provides a great outline of the basics of the NRQCD Lagrangian, fields, decays etc.

July 26, 2016February 19, 2017

Jets: More than Riff, Tony, and a rumble

Review Bite: Jet Physics
(This is the first in a series of posts on jet physics by Reggie Bain.)

Ubiquitous in the LHC’s ultra-high energy collisions are collimated sprays of particles called jets. The study of jet physics is a rapidly growing field where experimentalists and theorists work together to unravel the complex geometry of the final state particles at LHC experiments. If you’re totally new to the idea of jets…this bite from July 18th, 2016 by Julia Gonski is a nice experimental introduction to the importance of jets. In this bite, we’ll look at the basic ideas of jet physics from a more theoretical perspective. Let’
s address a few basic questions:

What is a jet? Jets are highly collimated collections of particles that are frequently observed in detectors. In visualizations of collisions in the ATLAS detector, one can often identify jets by eye.

A nicely colored visualization of a multi-jet event in the ATLAS detector. Reason #172 that I’m not an experimentalist...actually sifting out useful information from the detector (or even making a graphic like this) is insanely hard. — A nicely colored visualization of a multi-jet event in the ATLAS detector. Reason #172 that I’m not an experimentalist…actually sifting out useful information from the detector (or even making a graphic like this) is insanely hard.

Jets are formed in the final state of a collision when a particle showers off radiation in such a way as to form a focused cone of particles. The most commonly studied jets are formed by quarks and gluons that fragment into hadrons like pions, kaons, and sometimes more exotic particles like the $latex J/Ψ, Υ, χ_c and many others. This process is often referred to as hadronization.

Why do jets exist? Jets are a fundamental prediction of Quantum Field Theories like Quantum Chromodynamics (QCD). One common process studied in field theory textbooks is electron–positron annihilation into a pair of quarks, e⁺e^– → q q. In order to calculate the
cross-section of this process, it turns out that one has to consider the possibility that additional gluons are produced along with the qq. Since no detector has infinite resolution, it’s always possible that there are gluons that go unobserved by your detector. This could be because they are incredibly soft (low energy) or because they travel almost exactly collinear to the q or q itself. In this region of momenta, the cross-section gets very large and the process favors the creation of this extra radiation. Since these gluons carry color/anti-color, they begin to hadronize and decay so as to become stable, colorless states. When the q, q have high momenta, the zoo of particles that are formed from the hadronization all have momenta that are clustered around the direction of the original q,q and form a cone shape in the detector…thus a jet is born! The details of exactly how hadronization works is where theory can get a little hazy. At the energy and distance scales where quarks/gluons start to hadronize, perturbation theory breaks down making many of our usual calculational tools useless. This, of course, makes the realm of hadronization—often referred to as parton fragmentation in the literature—a hot topic in QCD research.

How do we measure/study jets? Now comes the tricky part. As experimentalists will tell you, actually measuring jets can a messy business. By taking the signatures of the final state particles in an event (i.e. a collision), one can reconstruct a jet using a jet algorithm. One of the first concepts of such jet definitions was introduced by Geroge Sterman and Steven Weinberg in 1977. There they defined a jet using two parameters θ, E. These restricted the angle and energy of particles that are in or out of a jet. Today, we have a variety of jet algorithms that fall into two categories:

Cone Algorithms — These algorithms identify stable cones of a given angular size. These cones are defined in such a way that if one or two nearby particles are added to or removed from the jet cone, that it won’t drastically change the cone location and energy
Recombination Algorithms — These look pairwise at the 4-momenta of all particles in an event and combine them, according to a certain distance metric (there’s a different one for each algorithm), in such a way as to be left with distinct, well-separated jets.

Figure 2: From Cacciari and Salam’s original paper on the “Anti-kT” jet algorithm (See arXiv:0802.1189). The picture shows the application of 4 different jet algorithms: the kT, Cambridge/Aachen, Seedless-Infrared-Safe Cone, and anti-kT algorithms to a single set of final state particles in an event. You can see how each algorithm reconstructs a slightly different jet structure. These are among the most commonly used clustering algorithms on the market (the anti-kT being, at least in my experience, the most popular).

Why are jets important? On the frontier of high energy particle physics, CERN leads the world’s charge in the search for new physics. From deepening our understanding of the Higgs to observing never before seen particles, projects like ATLAS,

An illustration of an interesting type of jet substructure observable called “N-subjettiness” from the original paper by Jesse Thaler and Ken van Tilburg (see arXiv:1011.2268). N-subjettiness aims to study how momenta within a jet are distributed by dividing them up into n sub-jets. The diagram on the left shows an example of 2-subjettiness where a jet contains two sub-jets. The diagram on the right shows a jet with 0 sub-jets.

CMS, and LHCb promise to uncover interesting physics for years to come. As it turns out, a large amount of Standard Model background to these new physics discoveries comes in the form of jets. Understanding the origin and workings of these jets can thus help us in the search for physics beyond the Standard Model.

Additionally, there are a number of interesting questions that remain about the Standard Model itself. From studying the production of heavy hadron production/decay in pp and heavy-ion collisions to providing precision measurements of the strong coupling, jets physics has a wide range of applicability and relevance to Standard Model problems. In recent years, the physics of jet substructure, which studies the distributions of particle momenta within a jet, has also seen increased interest. By studying the geometry of jets, a number of clever observables have been developed that can help us understand what particles they come from and how they are formed. Jet substructure studies will be the subject of many future bites!

Going forward…With any luck, this should serve as a brief outline to the uninitiated on the basics of jet physics. In a world increasingly filled with bigger, faster, and stronger colliders, jets will continue to play a major role in particle phenomenology. In upcoming bites, I’ll discuss the wealth of new and exciting results coming from jet physics research. We’ll examine questions like:

How do theoretical physicists tackle problems in jet physics?
How does the process of hadronization/fragmentation of quarks and gluons really work?
Can jets be used to answer long outstanding problems in the Standard Model?

I’ll also bite about how physicists use theoretical smart bombs called “effective field theories” to approach these often nasty theoretical calculations. But more on that later…